au sommaire
Un mètre pour mesurer les dimensions d'une pièce, une jauge de carburant pour estimer la quantité d'essence qu'il nous reste, des blocs qui nous renseignent sur l'état de charge de notre téléphone portable... Pour nous, représenter les nombres sur une ligne est une évidence. L'extrémité gauche correspondant au minimum tandis que la droite équivaut au maximum. À intervalles réguliers figurent les points intermédiaires.
Mais ce concept des nombres en ligne est-il inné ou l'apprend-on au cours de notre existence ? Certaines études affirment que cette capacité est inscrite en nous depuis des millions d'années. Cependant, il semble que les nourrissons n'aient pas tout à fait la même perception que les adultes. Ils conçoivent les nombres plutôt selon une échelle logarithmique, où plus les nombres sont grands et plus les écarts entre eux se resserrent. Il en va de même pour la tribu amazonienne des Mundurucus chez qui le sens des nombres a été testé par Stanislas Dehaene en 2008.
Le dogme semblait s'ébranler un peu. Il s'effondre complètement maintenant que Paul Nùñez et ses collègues de l'université de Californie, à San Diego, ont pu montrer que la tribu Yupno, perdue au milieu de la Papouasie-Nouvelle-Guinée, ne disposait pas de cette notion de nombres en ligne. Leurs résultats sont publiés dans Plos One.
Des Yupnos qui ne marchent pas en ligne
Les Yupnos sont environ 5.000 à vivre dans des petits villages, sans route et donc coupés du monde. La plupart des habitants ont suivi un enseignement scolaire, même léger, mais il n'existe aucune forme d'écriture native. Cependant, ils disposent d'un système numériquenumérique et possèdent des mots pour exprimer les nombres supérieurs à 20. Leur isolement fait d'eux des sujets idéaux pour étudier l'inné et l’acquis des mathématiques. Entre autres.
Pour réaliser leur étude, les chercheurs ont recruté 14 adultes qui n'avaient jamais été à l'école, et 6 qui l'avaient fréquenté quelque temps au moins. Un groupe contrôle de 10 Californiens a permis les comparaisons. Le test était simple. Il était demandé aux sujets de placer les nombres de 1 à 10 sur une ligne noire sur papier blanc, longue de 22 cm. Ces nombres étaient présentés de manière aléatoire, soit sous forme de sons préenregistrés dans le dialecte local, soit comme une séquence de sons ou bien par des points.
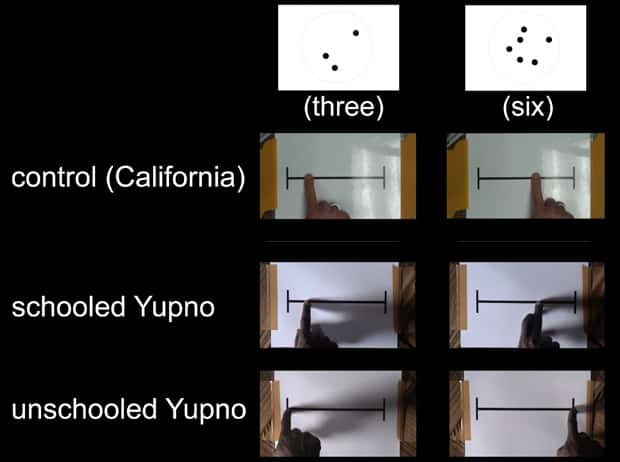
Ce schéma montre le genre de situation observée par les scientifiques. Pour les nombres 3 et 6, les contrôles et, dans certains cas les Yupnos scolarisés (schooled Yupno) plaçaient leur doigt sur la ligne, approximativement de la même façon. En revanche, les Yupnos qui ne sont jamais allés à l'école (unschooled Yupno) n'ont pas perçu le concept des nombres en ligne et désignaient du doigt l'une ou l'autre des extrémités. © Nùñez et al., Plos One
Les individus jamais scolarisés avaient un point commun : ils rangeaient les nombres soit tout à fait à gauche (pour les chiffres 1, et parfois 2 et 3), soit tout à fait à droite (pour tous les nombres strictement supérieurs à 3). Les Yupnos scolarisés avaient, eux, des résultats intermédiaires.
De la non-universalité des mathématiques
Les Yupnos étant toujours restés en dehors d'un quelconque système scolaire ont ignoré tous les points intermédiaires de la ligne, composant pourtant essentiel du concept de la représentation spatiale bidimensionnelle des nombres. Les chercheurs en concluent donc que c'est la culture qui nous inculque cette notion, et qu'elle n'est pas innée.
« Notre étude montre, pour la première fois, que le concept de nombres en ligne n'est pas une intuition universelle mais un outil culturel particulier qui requiert de l'entraînement et de l'éducation avant d'être maîtrisé » précise Paul Nùñez, qui assimile cette représentation des nombres à une métaphore propre à notre culture, utilisée notamment pour élaborer des systèmes de calculs plus sophistiqués.
« Les mathématiques à travers le monde - de l'Europe à l'Asie en passant par l'Amérique - sont enseignées comme un dogme, comme un fait objectif, noir ou blanc, vrai ou faux » poursuit le chercheur américain, alors que cela semble tout de même plus complexe. Il propose dans le même communiqué de presse de revisiter le statut des mathématiques, considérées, à tort selon lui, comme un langage universel.
























