au sommaire

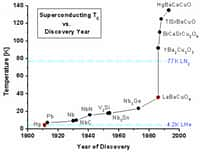
Magiquement, la théorie des trous noirs, celle de la supraconductivité et celle des collisions d'ions lourds conduisant à la formation d'un plasma de quarks-gluons sont mathématiquement liées par la théorie des cordes. Crédit : Nature
La théorie des supercordes dont la découverte remonte à la fin des années 1960 et au début des années 1970 a été souvent présentée ces dernières années comme un cul de sac de la physique basé sur d'obscures équations à la formidable complexité et dont les justifications physiques sont douteuses. A l'inverse, pour ses architectesarchitectes et ses partisans, il s'agit de la théorie du vingt-et-unième siècle tombée par hasard au vingtième, alors que les outils mathématiques et les concepts appropriés pour sa véritable compréhension restaient largement à développer.
Vers le milieu des années 1990 est arrivée la seconde révolution des supercordes et l'un de ses auteurs, le physiciensphysiciens argentin d'origine italienne Juan Maldacena, a été conduit, à l'aide de la théorie des supercordes, à une surprenante découverte en étudiant l'origine de l'entropie des trous noirs, et leur évaporation grâce au rayonnement Hawking.
De façon inattendue, les équations qu'il prenait en compte lui suggéraient une conjectureconjecture audacieuse, basée en partie sur des considérations déjà avancées par Léonard Susskind et Gérard ‘t Hooft. Pour la comprendre, quelques considérations préliminaires sont nécessaires.
Lorsque l'on considère un hologrammehologramme, toutes les informations sur l'image d'un objet en trois dimensions sont stockées sur une plaque en deux dimensions. Or dans le cas des trous noirs, les travaux de Bekenstein et Hawking avaient démontré que toute l'information perdue en y lançant des objets devait être reliée à la surface de ces derniers. L'état de la matièreétat de la matière tombant dans le volumevolume en 3D à l'intérieur d'un trou noir devait donc être encodé d'une façon mystérieuse sur la surface de son horizon en 2D.
En effet, un trou noir est une région de l'espace-tempsespace-temps close définie par un horizon dont rien, pas même la lumièrelumière, ne peut s'échapper. Cet horizon grandit avec la massemasse d'un trou noir. Si l'on y lance des bibliothèques entières, la masse du trou noir va donc croître et on verra augmenter la surface de l'horizon délimitant une région de l'espace dont le contenu en information devient indisponible pour un observateur extérieur.
Comme l'entropie peut être mise en liaison avec une perte d'information concernant un système physique, on comprend qu'une relation entre contenu en information dans le volume interne d'un trou noir et taille de son horizon est plausible, à défaut d'en comprendre toute la nature.

Juan Maldacena. Crédit : Stony Brook university
Juan Maldacena considérait initialement des trous noirs en 10 dimensions d'espace-temps plats (sauf là où se trouve un trou noir) et, à l'aide de la théorie des cordesthéorie des cordes, étudiait le comportement des champs de particules se propageant à proximité de leur horizon. Ses calculs suggéraient fortement que si l'on plaçait ces trous noirs à l'intérieur d'un modèle d'UniversUnivers à cinq dimensions d'espace-temps macroscopiques, caractérisé par une géométrie dite de anti-de Sitter et auquel étaient ajoutées cinq dimensions spatiales supplémentaires compactées selon des sphères (comme dans la théories de Kaluza-Klein), alors les détails des phénomènes se déroulant dans cet Univers, décrit par la théorie des cordes, étaient codés par le comportement de certains champs existant sur une frontière à l'infini de cet Univers.
Ces champs, ressemblant à ceux de la chromodynamique quantiquechromodynamique quantique, se propageaient uniquement sur cette frontière dont la géométrie est plate et en 4 dimensions d'espace-temps seulement.
En généralisant cette constatation, Maldacena aboutissait à sa célèbre conjecture stipulant que les équations de la théorie des cordes à 10D, décrivant n'importe quelle situation de gravitation quantiquegravitation quantique dans un espace-temps anti-de Sitter, sont reliées mathématiquement aux équations en espace-temps plat en 4D décrivant un champ de force analogue à celui décrit par les équations de Yang Mills de la QCD existant sur la frontière de cet espace-temps.
A ceci près que ces équations doivent être supersymétriques et posséder une symétrie supplémentaire liée à l'invariance par des transformations dites conformes. Celles-ci, dans un plan par exemple, ne respectent pas forcément les distances pour des figures géométriques mais conservent les angles.
L'aspect le plus spectaculaire de la conjecture dite aujourd'hui de Maldacena ou encore de correspondance AdS-CFT (pour anti-de-Sitter space/conformal field theory en anglais) n'est probablement pas que la gravitation en espace-temps courbe à 10 dimensions puisse être reliée à des sortes de champs électriqueschamps électriques en espace-temps plats à 4 dimensions. Bien que cela soit évidemment un résultat fort surprenant et hautement non trivial on peut tout de même sentir assez rapidemment comment cela est possible.
En effet, si l'on considère une surface courbe en deux dimensions et si l'on projette ses lignes de niveaux sur un plan, la modification de leur forme renseigne sur les modifications de courbure de la surface en deux dimensions. Si l'on considère que ces lignes de niveaux sont des lignes de champs électriques et magnétiques, on peut comprendre d'une façon intuitive, à défaut d'être rigoureuse, comment la géométrie courbe de l'espace-temps peut être reliée à un champ de force non gravitationnel en espace-temps plat.
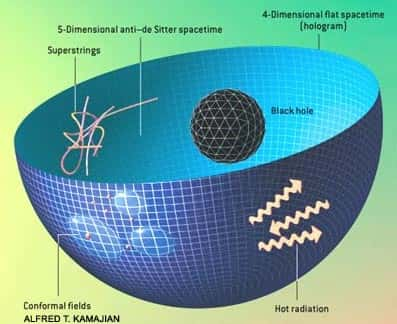
Via les équations de la théorie des cordes, la physique d'un trou noir dans un espace-temps Anti-de-Sitter à 5 dimensions est reliée à celle d'une théorie des champs conformes en 4 dimensions d'espace-temps sur la frontière de cet espace. Il s'agit d'un exemple du principe holographique de Sussking et 't Hooft. Crédit : universe-review
Non, le plus étonnant avec la conjecture de Maldacena est que des processus décrits par des équations classiques décrivant le comportement de certains champs autour d'un trou noir sont reliés à des processus quantiques semblables à ceux rencontrés avec des quarksquarks et des gluonsgluons dans les protonsprotons et autres hadronshadrons.
De fait, il semble bien que l'on arrive à mieux comprendre les expériences portant sur la formation du plasma de quarks-gluons en invoquant l'évaporation Hawking d'un trou noir décrite en grande partie par des équations classiques de supergravitésupergravité.
La frontière entre les équations de la mécanique quantiquemécanique quantique et des équations classiques décrivant une généralisation de la théorie de la relativité généralerelativité générale d'EinsteinEinstein devient floue et on a l'impression que derrière tout cela se cache une profonde unification de la physique réconciliant les points de vue d'Einstein et de Schrödinger avec ceux de Bohr et Heisenberg concernant la théorie quantique et l'unification des forces et des particules de la physique.
A défaut de prouver que l'espace-temps est bien à 10 ou 11 dimensions, les résultats obtenus dans les expériences de collisions d’ions lourds et la formation d’un plasma de quarks-gluons accréditent l'idée que la théorie des cordes est au moins un puissant moyen mathématique pour analyser les équations de la théorie quantique des champs.
On sait par exemple, en mécanique classique, que lorsque que l'on veut décrire le comportement de N particules, leurs équations de mouvementsmouvements permettent une analyse puissante des processus physiques qu'elles impliquent en introduisant un espace à 6N dimensions, celui des 3N coordonnées de positions et de 3N composantes de vitessesvitesses.
La géométrie de cet espace est décrite par les équations de la géométrie de Riemann pour les espaces courbes en 6N dimensions et cela n'impliquait pas que l'espace lui-même soit courbe et à 6N dimensions. La situation est similaire ici.
Il se trouve que les méthodes de la théorie quantique des champs sont utiles pour comprendre la physique du solidesolide et voilà longtemps que les physiciens du solide profitent des correspondances entre les équations et les méthodes de la physique des hautes énergiesénergies et celles de leur domaine. Inversement, les théoriciens des particules élémentairesparticules élémentaires profitent parfois eux aussi des découvertes faites par leurs collègues. La théorie moderne de la renormalisation et le boson de Higgsboson de Higgs lui-même doivent leur existence initialement à des travaux en physique de la matière condensée.
Depuis quelques années déjà, des physiciens sont en train d'étudier des extensions de la conjecture de Maldacena pour relier mathématiquement la théorie des cordes, grande consommatrice de ce qu'on appelle la théorie des champs conformes, avec la physique de la matière condensée qui en fait aussi un très grand usage dans le cas des problèmes de transition de phasetransition de phase, dont le plus emblématique est peut-être celui de la supraconductivitésupraconductivité.

Jan Zaanen. Crédit : The Regents of the University of California / UC Santa Barbara, Kavli Institute for Theoretical Physics
« Les calculs collent parfaitement »
Jan Zaanen fait partie de ces physiciens qui se demandent justement depuis quelques années si des percées dans le domaine de la supraconductivité à haute température critiquetempérature critique ne sont pas possibles du point de vue théorique grâce à la théorie des cordes et à la correspondance AdS-CFT. Il a donc entrepris d'étudier la théorie des cordes ainsi qu'une collaboration avec un expert du domaine venant d'arriver dans son Université de Leiden, Koenraad Schalm.
Rappelons que si la supraconductivité ordinaire est bien décrite par la théorie BCS, celle se produisant à plusieurs dizaines de kelvinskelvins dans des matériaux comme les cupratescuprates reste encore très mal comprise. Elle échappe en particulier à la théorie BCS et nombreux sont les théoriciens qui voudraient en comprendre l'origine.
Zaanen et Schalm se sont mis au travail avec Mihailo Cubrovic. D'après les spécialistes de la supraconductivité à haute température critique, une bonne hypothèse de travail est celle faisant intervenir l'idée que les électronsélectrons dans un cuprate devenant supraconducteursupraconducteur sont décrits par ce que l'on appelle un liquideliquide quantique de Fermi dans un état critique.
La description de ce liquide est difficile mais selon la conjecture de Maldacena étendue à la physique du solide, son comportement quantique est relié à celui des électrons autour d'un trou noir chargé de Reisner-Nordström plongé dans un espace-temps anti-de Sitter avec une constante cosmologiqueconstante cosmologique. Il existe alors un dictionnaire reliant les solutions des équations décrivant les deux systèmes physiques et des calculs dans un cas peuvent être plus faciles.

Koenraad Schalm. Crédit : Stony Brook university
Le résultat des travaux des chercheurs est probablement le mieux décrit par les déclaration de Zaanen : « c'est magnifique, je n'ai jamais éprouvé une tel état d'euphorieeuphorie ! Nous n'espérions pas que cela marcherait si bien. Les calculs mathématiques collent parfaitement. Quand nous avons vu les résultats des calculs, au début, nous ne pouvions pas le croire ».
Le mystère de la supraconductivité à haute température critique n'est toujours pas résolu mais comme les chercheurs s'y attendaient, les calculs ont effectivement montré l'émergenceémergence d'un liquide de Fermi en relation avec une transition de phase quantique lié à la supraconductivité.
Encore une fois, cela ne prouve pas que la théorie des cordes est bien la bonne théorie de la gravitation quantique et la bonne théorie du Tout, la Theory Of Everything selon les mots de John Ellis. Mais les preuves s'accumulent, qui montrent sa pertinence et sa puissance en tant qu'outil d'analyse mathématique des équations des théories quantiques des champs et de la matière condensée.
Ceux qui persistent à dire que la théorie n'a jamais rien produit qui puisse être observé au laboratoire vont avoir de plus en plus de mal à être crédibles...