Gravitation quantique à boucles : qu'est-ce que c'est ?

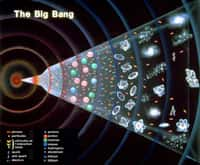
La gravitation quantique à boucles est l'une des principales voies de recherche concernant le problème de l'élaboration d'une théorie capable de décrire l'aspect quantique de la gravitation. Il faut en effet une théorie quantique de la gravitation lorsque l'on veut comprendre la naissance de l'univers et ce qui se passe à l'intérieur des trous noirs. Dans le cadre de la relativité générale classique, il apparaît alors dans ces situations des singularités avec des divergences de certaines quantités physiques indésirables. L'exigence d'une homogénéité des lois de la physique demande elle aussi l'unification des lois de la mécanique quantiquemécanique quantique avec celles de la dynamique de l'espace-tempsespace-temps. C'est pourquoi les physiciensphysiciens théoriciens cherchent depuis des décennies une mythique théorie de la gravitation quantique.

Le sujet de la gravitation quantique est extrêmement vaste et il faudrait probablement des centaines de pages pour lui rendre justice. Il est bien connu que l'applicationapplication de la mécanique quantique aux équationséquations de la relativité générale d'EinsteinEinstein conduit à des divergences infinies lorsqu'on cherche à coupler le champ de gravitation à la matièrematière. Il existe toutefois des situations où l'on peut faire des calculs approximatifs de gravitation quantique sans que des quantités infinies incontrôlables n'émergentémergent. C'est le cas dans certains modèles de cosmologiecosmologie simples décrits par ce qu'on appelle la gravitation quantique canonique et introduits dans les années 1960 par John Wheeler et surtout Bryce DeWitt pour l'essentiel.

La cosmologie quantique

En résumé, on cherche à appliquer les règles de quantification standards dites canoniques aux équations d'Einstein, ce qui veut dire qu'on cherche à mettre ces dernières sous une forme dite hamiltonienne bien connue avec la mécanique analytique. Il faut pour cela introduire, comme pour la mécanique d'un système de particules, un espace de phases et une fonction hamiltonienne H représentant l'énergieénergie totale du système champ de gravitation+matière. De même qu'un point dans l'espace des phasesespace des phases représente un ensemble de positions-impulsions possibles pour des particules en mouvementmouvement sous l'action de forces, un point dans l'espace des phases du champ de gravitation représentera un état possible de la géométrie de l'espace-temps courbé par la présence de matière, et plus généralement d'impulsions et d'énergies. On a nommé cet espace de configurationsespace de configurations de l'espace-temps : le superespace (à ne pas confondre avec celui de la supergravitésupergravité).

On peut alors construire une équation de Schrödingeréquation de Schrödinger avec une fonction d'onde dont le carré donne la probabilité de trouver la géométrie de l'espace-temps dans un état donné. C'est justement l'équation de Wheeler-DeWitt. Le problème est que, contrairement au cas avec N particules, la géométrie de l'espace-temps est décrite par un champ de tenseurtenseur à 10 composantes défini en chaque point de l'espace-temps. Comme il y en a une infinité, on comprend aisément que la résolutionrésolution d'une telle équation n'est pas chose facile. Cependant, si l'on fixe par avance une classe de géométries possibles ne dépendant que d'un petit nombre de paramètres, certains calculs sont alors possibles. Cela revient à tronquer l'espace des phases précédant en « gelant » des degrés de liberté pour ne plus garder qu'un mini superespace. 

Sur une sphère, le transport d'un vecteur tangent à une courbe parallèlement à elle-même le long d'une boucle ne ramène pas à l'identique ce vecteur. On voit ainsi que les orientations d'un vecteur tangent transporté parallèlement du pôle Nord selon le trajet NBA et selon le trajet NA diffèrent d'un angle α. Sur une surface plane, cet angle serait nul. En considérant sur un espace-temps courbe un ensemble de boucles de ce genre, la connaissance des résultats des calculs des transports parallèles de vecteurs le long de ces boucles caractérise la courbure de l'espace-temps et sa forme. C'est le traitement quantique de ces boucles qui est utilisé pour faire de la gravitation quantique à boucles. © Luca Antonelli-wikipedia

Le cas le plus simple est celui où l'on prend les modèles cosmologiques homogènes et isotropesisotropes de Friedman-Robertson-Walker (FRW) avec comme origine du champ de gravitation le champ le plus simple qu'on puisse imaginer : un champ scalaire  décrit par une équation de Klein-Gordon avec un potentiel V()). L'évolution dans le temps du champ de gravitation se réduit ici à un seul degré de liberté a(t). La fonction hamiltonienne du système prend alors une forme similaire à celle décrivant une particule avec deux coordonnées de position, ici a(t) et (t), se déplaçant dans un potentiel compliqué. Les règles de quantificationquantification d'un tel système sont bien connues en mécanique ondulatoiremécanique ondulatoire et l'équation quantique décrivant ces modèles simples d'univers n'est pas plus compliquée, mais pas moins, que celles que l'on peut rencontrer en physique atomique et moléculaire.

Le problème de la singularité cosmologique initiale

Comme on l'avait laissé entendre précédemment, dans le cadre de la relativité générale classique, les modèles de FRW sont problématiques, avec bien d'autres d'ailleurs, car l'on peut montrer que lorsque t=0 la courbure de l'espace-temps devient infinie. La notion même d'espace-temps s'effondre, bloquant tout. Le début de l'univers, si cette notion même a un sens, est alors complètement hors de portée de la connaissance humaine. De même, une situation identique se produit lorsqu'une étoileétoile s'effondre pour donner un trou noir en RG classique, une singularité de l'espace-temps se forme et les lois de la physique s'y brisent.

Or, ce n'est pas la première fois que la physique a été confrontée à ce genre de problème. Déjà, lors de la constructionconstruction des premiers modèles d'atomesatomes, l'électronélectron tournant autour du noyau était en situation instable et devait finir par s'effondrer sur le noyau en créant là aussi une singularité, mais pas d'espace-temps. L'introduction de la mécanique quantique et de la mécanique ondulatoire avec une fonction d'onde, avaient alors montré qu'il n'existait qu'une série d'états dynamiques discrets accessibles à l'électron, les fameux niveaux d'énergie de l'atome de Bohratome de Bohr. La fonction d'onde décrivant la probabilité de trouver l'électron dans une région de l'espace « étalait » cette même position en rendant l'effondrementeffondrement précédent impossible.

John Wheeler et Bryce DeWitt avaient très clairement indiqué qu'un processus similaire devait se produire avec leur équation de Schrödinger de l'espace-temps. Les singularités en relativité générale seraient donc probablement « lissées » par le traitement quantique, stoppant ainsi leur formation.

Des résultats en ce sens avaient d'ailleurs été fournis dès la fin des années 1960 et surtout dans le cadre du fameux modèle avec temps imaginaire de Hartle-Hawking au début des années 1980. Malheureusement, comme indiqué précédemment, à chaque fois il s'agissait d'une situation très particulière où l'on admettait que la géométrie de l'univers ne pouvait pas s'écarter beaucoup d'une certaine forme d'homogénéité et d'isotropieisotropie permettant de simplifier considérablement les calculs. Cela n'est pas satisfaisant car de telles hypothèses, bien que justifiables par certains côtés, n'en sont pas moins des vœux pieux. La théorie devrait partir d'un espace-temps arbitraire, non prédéterminé en partie par avance, et ce sont les calculs qui fourniront l'état de cet espace-temps.

Il faudrait pour cela résoudre l'équation de Wheeler-DeWitt de manière générale ou au mieux générique, mais comment s'y prendre ?

Variables d'Ashtekar et boucles

Une percée considérable s'est faite au milieu des années 1980. Le physicien d'origine indienne Abhay Ashtekar, qui avait été le post-doc du grand Roger PenroseRoger Penrose, a introduit une formulation des équations d'Einstein dans l'espace des phases de l'espace-temps simplifiant considérablement leur formulation hamiltonienne. En fait, il montrait que l'on se trouvait dans une situation formellement très proche de celle que l'on obtenait avec les équations de Yang-MillsYang-Mills, notamment celle de la QCD. Les techniques issues de cette théorie de jaugethéorie de jauge des interactions nucléaires fortes, la chromodynamique quantiquechromodynamique quantique, pouvaient alors être transposées. 

Plus précisément, il apparaissait que les bonnes variables à utiliser étaient liées à ce qu'on appelle des holonomies, des quantités qui se calculent avec des transports parallèles de vecteur le long de boucles dans l'espace-temps.

Les travaux de Carlo Rovelli l'ont conduit à découvrir que la LQG prédisait une structure discrète pour l'espace-temps au voisinage de l'échelle de Planck. © John Baez

À défaut d'une solution générale de l'équation de WDW, Lee Smolin et Carlo Rovelli réussirent à trouver de grandes classes de solutions de l'équation de Wheeler-DeWitt mais surtout, ils réussirent à préciser de façon rigoureuse l'espace des solutions de cette équation.

Comme toutes les équations de Schrödinger, les solutions de ces équations peuvent être rassemblées en un espace vectoriel abstrait ressemblant à l'espace habituel, il s'agit du célèbre espace de Hilbert.

Une solution est alors décrite par un point dans cet espace repéré par un « vecteur position ». Dans le langage de la mécanique quantique, les fonctions d'ondes correspondant à une géométrie particulière de l'espace-temps sont des vecteurs d'états. Le principe de superposition des états de la mécanique quantique implique alors que la géométrie de l'espace-temps peut se trouver sous la forme d'une superposition d'états donnée par la somme vectorielle de ces vecteurs.

Le résultat le plus spectaculaire fut qu'il était alors possible de construire des opérateurs de surface et de volumevolume, pour la géométrie de l'espace-temps, dont les spectresspectres sont discrets !

Un espace-temps discret pour la cosmologie et l'entropie des trous noirs

On sait qu'en mécanique quantique les grandeurs comme l'énergie ou le moment cinétiquemoment cinétique sont données par des opérateurs. En agissant sur la fonction d'onde, qui mathématiquement ressemble à la fonction décrivant une onde lumineuse, l'opérateur d'énergie extrait alors les différentes composantes du spectre composant cette onde. Dans le cas de l'atome d'hydrogènehydrogène, cela donne des niveaux discrets d'énergie et des orbitesorbites caractérisées elles aussi par une série discrète de distances de l'électron par rapport au noyau.

La situation est vraiment très similaire car le principe de correspondance de Bohrprincipe de correspondance de Bohr s'applique aussi dans le cas du spectre des aires et des volumes. Au fur et à mesure que le nombre quantiquenombre quantique caractérisant des orbites de plus en plus grandes augmente, la différence entre les niveaux d'énergie devient de plus en plus faible ainsi que les distances spatiales séparant les orbites. Le spectre discret devient continu et la physique quantiquephysique quantique se raccroche à la physique classique. Ainsi, pour des surfaces et des volumes de plus en plus grands, la notion d'espace-temps classique continu est retrouvée.

Martin Bojowald a été un des premiers à tirer les conséquences en cosmologie de ce caractère discret de l'espace-temps à l'échelle de PlanckPlanck fourni par les équations de la LQG. Il a alors appliqué celles-ci aux modèles de FRW précédents et il a découvert plusieurs choses.

Même si l'on reste toujours dans une approximation de mini superespace, la situation est bien mieux contrôlée, car, le fait que la géométrie de l'espace-temps soit discrète réduit déjà considérablement le nombre de degrés de liberté possibles pour l'espace-temps à l'approche de la singularité primordiale. Ce qui permet de mieux justifier l'utilisation des mini superespaces en raison même de la structure de la LQG.

On trouve alors que l'on peut définir un opérateur de courbure pour l'espace-temps et un opérateur de « position » a(t) pour le facteur décrivant l'expansion des univers de FRW. Contrairement aux résultats obtenus avant la LQG, le spectre de ces opérateurs est discret.

Étonnamment, alors que le spectre du dernier opérateur possède la valeur 0 correspondant à un volume nul, celui de la courbure possède alors une borne maximale, la singularité de l'espace-temps est éliminée !

On peut alors prolonger sans aucun problème la structure de l'espace-temps avant ce qui correspond pour nous à un temps 0. Il y a alors un « avant Big BangBig Bang ». Si l'on représente le facteur d'expansion de l'univers au cours du temps, celui-ci effectue un mouvement rappelant celui d'une balle rebondissant éternellement de façon élastique, on parle d'ailleurs en anglais de « bouncing Univers » pour des théories de ce genre. On pourrait croire que chaque cycle d'expansion-contraction reproduit l'univers à l'identique mais Bojowald fait remarquer que ces équations quantiques rendent en partie indéterminés les paramètres décrivant chaque nouveau cycle qui perdrait donc à chaque fois une partie des informations caractérisant l'état précédant.  

Le caractère discret des aires en LQG a aussi été utilisé pour retrouver la relation entre l'entropieentropie d'un trou noir et la valeur de l'aire de l'horizon de ce trou noir. Un résultat qui avait été obtenu précédemment par la théorie des cordesthéorie des cordes dans le cas de certains trous noirs supersymétriques. En LQG, le résultat est cependant valable directement pour un trou noir de Schwarzschild, du type de ceux que l'on sait exister dans la nature.

Champ lexical : lQG | loop Quantum Gravity | gravitation quantique