au sommaire
L'espace des phases en mécanique analytique est un espace à 2M dimensions permettant d'interpréter géométriquement le mouvement d'un système mécanique décrit par des équations différentielles du second ordre par rapport au temps. Il est étroitement associé aux équations de Hamilton et donc au formalisme HamiltonienHamiltonien. Les 2M dimensions correspondent aux M paires de variables conjuguées intervenant dans les équations différentielles gouvernant le mouvement d'un système mécanique (un exemple simple est donné ci-dessous).
Cet espace est fondamental en physique et on le retrouve au coeur de la formulation de la mécanique quantique et de la mécanique statistique.
Initialement introduit dans des problèmes de mécanique céleste, pour décrire de manière unifiée les équations de la mécanique des points matériels dans un potentiel et les trajectoires des rayons lumineux dans des milieux inhomogènes d'indices variables, Schrödinger en fera usage pour construire la mécanique ondulatoiremécanique ondulatoire à partir des idées de De Broglie. Auparavant, Bohr et Sommerfeld l'avaient utilisé en théorie quantique pour exprimer des règles de quantificationquantification de systèmes mécaniques simples.

Henri Poincaré (1854-1912)
Poincaré fera lui aussi un grand usage de cet espace pour introduire des raisonnements géométriques en mécanique céleste et pour étudier le problème des trois corps. Ces études seront à la base de la théorie du chaos.
Concrètement, dans l'exemple d'un gazgaz constitué de N particules, l'espace des phases sera à 6N=2M dimensions. On aura 3N coordonnées de position et 3N coordonnées de quantité de mouvementquantité de mouvement
. Ces coordonnées sont dites généralisées car elles peuvent correspondre à différents systèmes de coordonnées cartésiens, sphériques, hyperboliques etc...
Plus généralement, les coordonnées généralisées et
représentent des variables conjuguées d'un système mécanique arbitraire. Dans le cas d'un gyroscopegyroscope, d'une toupie ces coordonnées seront des angles dans le premier cas et des moments cinétiquesmoments cinétiques dans le second.
La trajectoire d'un système mécanique est donc représentée par celle d'un point à 2M coordonnées dans l'espace des phases. Si l'on considère différentes conditions initiales, on aura différentes courbes dans cet espace. Dans le cadre de la mécanique statistique cela permettra d'étudier le comportement moyen d'un ensemble de systèmes mécaniques identiques sous la forme d'un fluide de particules. En théorie du chaos, l'espace des phases permet de visualiser que les trajectoires de systèmes non-linéaires avec différentes conditions initiales se retrouvent parfois proches de certaines formes géométriques dans cet espace. On parle alors d'attracteur étrange car tout se passe comme si ces formes étranges attiraient les points représentant un système mécanique pour les forcer à rester dans leur voisinage.
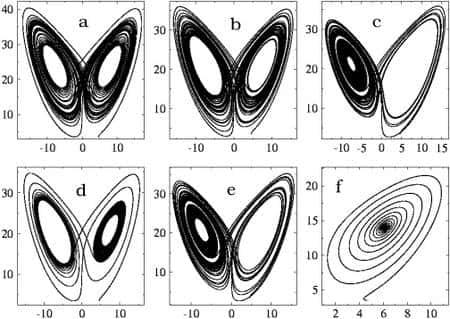
Trajectoires dans l'espace des phases représentant l'attracteur étrange de Lorenz en 2D
Crédit :Josep Sardanyés Cayuela
La théorie géométrique de l'espace des phases fait intervenir la théorie des groupes et elle permet de ramener des théorèmesthéorèmes de mécanique à des théorèmes de géométrie. On parle de géométrie symplectique et celle-ci intervient dans les formulations géométriques de la mécanique quantique.
La théorie de l'espace des phases n'est pas limitée à des systèmes physiques discrets constitués d'un nombre fini de degrés de liberté. On peut la généraliser pour l'appliquer à la théorie des champs et c'est ce qui a été fait en relativité générale et en théorie des champs de Yang-MillsYang-Mills des particules élémentairesparticules élémentaires.
Pour aller plus loin :























