au sommaire

De gauche à droite, Chen Ning Yang et Robert Mills en pleine discussion à la fin des années 1990. Mills est décédé en 1999. © Nu Xu
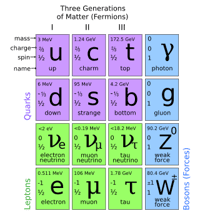
Les théories de Yang-Mills sont une famille de théories des champs basées sur la notion d'invariance de jauge, utilisée pour décrire les champs de force fondamentaux en physique. On peut aussi les utiliser pour classifier topologiquement des espaces que l'on appelle des variétés en mathématiques, comme Simon Donaldson l'a montré en 1982. Elles tirent leur nom d'une théorie quantique des champs relativiste proposée en 1954 par Chen Ning Yang et Robert Mills pour décrire les forces nucléaires fortes entre protons et neutrons.

De gauche à droite, les physiciens théoriciens Chen Ning Yang et Robert Mills. Yang a décroché le prix Nobel de physique pour ses travaux sur la violation de la parité en compagnie de Tsung-Dao Lee en 1957. © AIP
Des équations de Maxwell à la chromodynamique quantique
Les équations des théories de Yang-Mills généralisent celles de Maxwell en utilisant la théorie des groupes de Sophus Lie, héritières de la théorie des groupes d'Évariste Galois. Elles sont généralement non linéaires, comme les équations de la relativité générale qui peuvent être vues comme un cas particulier des équations de Yang-Mills. Généralement, les groupes de Lie utilisés sont de type dit SU(N). La chromodynamique quantiquechromodynamique quantique repose sur le groupe SU(3) et la théorie électrofaiblethéorie électrofaible fait intervenir deux groupes, U(1) pour l'électromagnétismeélectromagnétisme et SU(2) pour les forces nucléaires faiblesforces nucléaires faibles. Ces groupes, qui décrivent les propriétés de symétrie des équations de Yang-Mills, impliquent des lois de conservation avec des quantités conservées qui généralisent celle de la charge électrique.
C'est le grand mathématicienmathématicien Hermann Weyl qui s'est aperçu que la notion d'invariance de jauge, décrite au moyen des groupes de Lie, était profonde en théorie quantique. Il s'en est aperçu d'abord en cherchant une description géométrique unifiée de la gravitationgravitation et de la force électromagnétique vers 1919, puis une description de l'électrodynamique quantiqueélectrodynamique quantique dans le cadre de la théorie des groupes. Dans le cas des équations de Maxwelléquations de Maxwell, cette invariance de jauge correspondait au fait qu'il était possible de changer d'une certaine façon les valeurs de ce qu'on appelle le potentiel vecteur dans ces équations, sans changer la forme desdites équations. Comme on peut généraliser cette propriété avec les équations des champs de Yang-Mills, on parle parfois aussi de théories de jaugethéories de jauge ou de champs de jaugechamps de jauge pour les théories de Yang-Mills.

Le grand mathématicien et physicien Hermann Weyl, le plus doué des élèves de Hilbert, a beaucoup fait pour montrer l'importance des groupes en physique quantique. On lui doit aussi un excellent petit livre de vulgarisation sur le concept de groupe (Symétrie et mathématique moderne) et les connexions avec la notion de symétrie dans les sciences de la nature, qu’il s’agisse de la cristallographie, de la biologie ou de la théorie de la relativité, voire du domaine artistique. © ETH Zurich
Un cadre pour la théorie quantique des champs relativistes
Lorsque l'on cherche à combiner les lois de la relativité et celles de la mécanique quantiquemécanique quantique pour décrire des champs de force, on s'aperçoit que la forme la plus naturelle des équations décrivant ces champs doit être celle d'une théorie de Yang-Mills où des généralisations des photonsphotons des équations de Maxwell émergentémergent naturellement.
Malheureusement, ces nouvelles particules apparaissaient comme nécessairement sans massemasse, et donc de portée infinie, en contradiction avec celles des forces nucléaires faibles et fortes. Il a fallu attendre la découverte du mécanisme de Brout-Englert-Higgs (BEH) avec le champ et le bosonboson de Higgs associés pour que l'on puisse construire des modèles de théorie quantique des forces nucléaires débarrassés de cet obstacle. Une théorie unifiée des forces électromagnétique et nucléaire faible basée sur les équations de Yang-Mills a ainsi pu être proposée en 1967 par Steven WeinbergSteven Weinberg et indépendamment par Abdus SalamAbdus Salam.

En utilisant les travaux de Richard Feynman et surtout de Martinus Veltman, le prix Nobel Gerard 't Hooft (à l’image) a prouvé que les théories de Yang-Mills complétées par le mécanisme de Brout-Englert-Higgs étaient renormalisables. On pouvait réguler des quantités divergentes infinies pour faire des calculs finis dans ce qui est appelé aujourd'hui le modèle standard de la physique des particules. © Wammes Waggel, Wikipédia
Théories de grande unification et supersymétrie
Toutefois, il a aussi fallu attendre le début des années 1970 pour que Martinus Veltman et surtout Gerard 't Hooft prouvent que les théories de Yang-Mills complétées par le mécanisme BEH étaient libres du fameux problème des divergences infinies rencontré en théorie quantique des champs relativiste la première fois dans le cadre de l'électrodynamique quantique. Cela a ouvert la voie aux travaux théoriques et expérimentaux des années 1970 à 2010, débouchant sur le modèle standardmodèle standard actuel en physique des particules.
Les théories de jauge sont toujours au cœur de bon nombre de travaux en physique théorique, et même en mathématique pure. Elles ont servi à construire des théories unifiées de toutes les forces comme les théories de grande unification (GUTGUT) et la théorie des supercordesthéorie des supercordes. Combinées à la supersymétriesupersymétrie, elles deviennent les théories de Yang-Mills supersymétriques intensément utilisées pour explorer la fameuse mais mystérieuse correspondance de Maldacena.