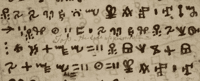au sommaire
Passons à un deuxième moment d'histoire des mathématiques.
Nous avons l'habitude de penser que la manière dont nous désignons les objets mathématiques, comme les objets de la vie courante, est un détail. Il n'y a pas de raison d'appeler « lionlion » un lion ou « tigretigre » un tigre. Nous aurions pu choisir deux autres mots et, pourvu que nous employions tous la même convention, toutes les conventions se valent. Les linguistes, pour qualifier ce phénomène, parlent du caractère « arbitraire » du signe. De même, nous aurions pu décider d'utiliser un autre nom que « trois » pour le nombre trois et un autre symbole que « 3 » pour l'écrire, sans que cela change grand-chose.

© Geralt, Pixabay
D'autres langues utilisent bien d'autres mots, drei ou three, et leurs mathématiques sont pourtant les mêmes que les nôtres. En poussant plus loin cette thèse de l'arbitraire du signe, on peut penser que le fait que l'on écrive le nombre trente et un « trente et un », « IIIIIIIIIIIIIIIIIIIIIIIIIIIIIII », « XXXI », « 3X 1I » ou « 31 » est indifférent. Ce n'est cependant pas tout à fait le cas. Tout d'abord, d'où nous vient ce besoin d'un langage spécial pour écrire les nombres ? Dans les sciences, comme ailleurs, on donne des noms aux objets que l'on utilise et, en général, cela ne nécessite pas l'invention d'un langage particulier. Par exemple, pour nommer les éléments chimiques, on a inventé un nom différent pour chacun d'eux : hydrogène, hélium... tout en continuant à utiliser le français. Mais les éléments chimiques, même s'ils sont nombreux, sont en nombre fini. On a, de même, introduit un nom particulier pour chacun des petits nombres : « un », « deux », « trois »... et même un symbole spécial : « 1 », « 2 », « 3 »... mais, contrairement aux éléments chimiques, les nombres sont une infinité : il est impossible de leur donner un nom à chacun, car un langage doit avoir un nombre fini de symboles et de mots.
Ainsi est née l'idée d'exprimer les nombres non avec un nombre infini de symboles mais en combinant un nombre fini de symboles, c'est-à-dire d'inventer non un lexique mais une grammaire, donc un langage. Or, si le lexique est arbitraire, la grammaire l'est beaucoup moins et certaines grammaires du langage des nombres sont plus pratiques que d'autres pour raisonner et pour calculer. Parmi les écritures « trente et un », « IIIIIIIIIIIIIIIIIIIIIIIIIIIIIII », « XXXI », « 3X 1I » et « 31 », la dernière, dans laquelle le fait que le chiffre 3 représente un nombre de dizaines est indiqué par sa position, est la meilleure. Car, quand on écrit deux nombres l'un sous l'autre, elle aligne les unités avec les unités, les dizaines avec les dizaines... ce qui permet des algorithmes simples pour faire des additions et des soustractions. Mais c'est surtout l'algorithme de la multiplication qui est simplifié, puisque, pour multiplier un nombre par 10, il suffit d'ajouter un 0 la fin, c'est-à-dire de décaler les chiffres d'un cran vers la gauche.
Cette écriture positionnelle vient de Mésopotamie où des ébauches en étaient déjà utilisées 2000 ans avant notre ère. Cependant, les Mésopotamiens utilisaient un système trop compliqué, qui a été simplifié ensuite par les mathématiciensmathématiciens indiens. Ce système indien a, par la suite, été diffusé dans le monde arabe à partir du IXe siècle, en particulier grâce au livre Le Calcul Indien écrit par Abu Ja'far Muhammad ibn Musa al-Khwarizmi, dont le nom a donné le mot « algorithme ». Ce système s'est ensuite diffusé en Europe à partir du XIIe siècle. Les mathématiciens du Moyen Âge ont donc reçu un double héritage : celui des Grecs, mais aussi, à travers cette question de l'écriture positionnelle, celui des Mésopotamiens, au moins aussi important que le premier. Ces mathématiciens ont alors passé plusieurs siècles à concevoir et améliorer les algorithmes. Loin d'avoir été étouffée par la découverte de la méthode axiomatique, la problématique du calcul, à travers cet héritage des mathématiques mésopotamiennes, est restée bien vivante dans les préoccupations des mathématiciens du Moyen Âge.