Le calcul intégral

Après l'algorithme d'EuclideEuclide et les algorithmes pour les opérations arithmétiques, passons à un troisième moment de l'histoire des mathématiques : le calcul intégral, qui s'est développé au XVIIe siècle avec les travaux de Bonavantura Cavalieri, Isaac NewtonIsaac Newton, Leibniz... mais dont les prémices remontent à l'Antiquité, avec deux résultats dus à ArchimèdeArchimède portant l'un sur l'aire du disque et l'autre sur l'aire du segment de parabole.

Bonabantura Cavalieri. © G. Dallorto, wikimedia commons, DP

On sait aujourd'hui que l'aire d'un disque s'obtient en multipliant le carré de son rayon par un nombre qui vaut 3,1415926... Archimède n'a pas été si loin, mais il a démontré que cette aire était comprise entre 3 + 10/71 = 3,140... et 3 + 1/70 = 3,142... fois le carré du rayon. Autrement dit, il a déterminé les deux premières décimales du nombre π. Dans le cas du segment de parabole, en revanche, Archimède est parvenu à un résultat exact : l'aire d'un tel segment est égale à quatre tiers fois l'aire du triangle inscrit dans ce segment.

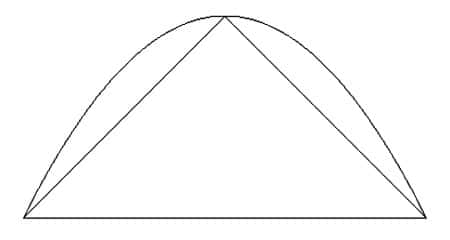
Pour parvenir à ce résultat, Archimède a décomposé le segment de parabole en une infinité de petits triangles dont il a ajouté les aires.

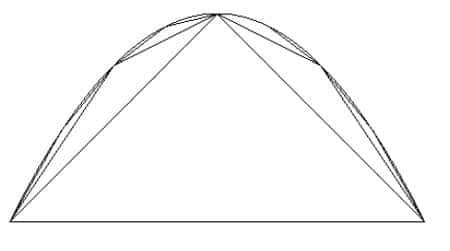
En prenant comme unité l'aire du triangle inscrit dans le segment de parabole, le premier triangle a, par définition, une aire égale à 1. On peut démontrer que les deux petits triangles sur ses côtés ont une aire totale égale à 1/4, que les quatre petits triangles de l'étape suivante ont une aire égale à 1/16... Chaque ensemble de triangles a une aire totale égale au quart de celle de l'ensemble précédent. L'aire du segment de parabole s'obtient en ajoutant l'aire de tous ces triangles : 1 + (1/4) + (1/4)² + (1/4)³ + ... et la somme de cette infinité de nombres donne un résultat fini : 4/3. Archimède, qui avait une certaine réticence à ajouter une infinité de nombres, s'est contenté de considérer les additions finies 1, 1 + (1/4), 1 + (1/4) + (1/4)²... qui donnent les aires de polygones inscrits dans le segment de parabole, donc qui sont toutes inférieures à l'aire du segment de parabole lui-même. Il a montré que l'aire du segment de parabole ne peut pas être inférieure à 4/3 car l'aire du segment de paraboles serait alors inférieure à celle de l'un de ces polygones, ce qui est impossible. Par un autre argument qui s'appuyait, quant à lui, sur les polygones circonscrits, Archimède a montré que l'aire du segment de parabole ne peut pas être supérieure à quatre tiers. Si elle n'est ni supérieure à quatre tiers, ni inférieure à quatre tiers, cette aire ne peut être qu'égale à quatre tiers.

Ce détour de raisonnement a été supprimé au XVIe siècle quand des mathématiciensmathématiciens comme Simon Stévin et François Viète ont commencé à utiliser des additions d'une infinité de nombres. Mais, même simplifié, le raisonnement d'Archimède demande de démontrer que l'aire totale de chaque famille est le quart de celle de la famille précédente, un tour de force qui fait que, jusqu'au XVIIe siècle, la détermination de l'aire de chaque figure était un véritable casse-tête.

Au XVIIe siècle, après l'introduction de la notion de coordonnée par René DescartesRené Descartes, on décrit volontiers une courbe par son équation, par exemple, la parabole de la figure précédente par l'équation y = 1 - x².

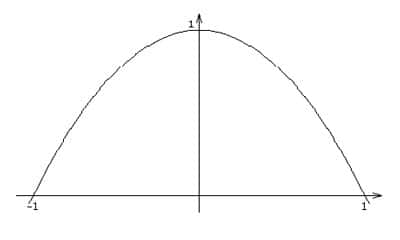
Connaissant cette équation, on peut se demander s'il n'y a pas un moyen de calculer l'aire du segment de parabole, c'est-àdire l'aire comprise entre la courbe et l'axe horizontal, sans recourir à cette décomposition en triangles. Une des grandes découvertes des mathématiciens du XVIIe siècle a précisément porté sur la méthode qui permet de calculer l'aire d'une figure ainsi délimitée par une courbe dont on connaît l'équation, pourvu que cette équation soit suffisamment simple.

Le premier pas vers cette découverte a consisté en la mise en évidence d'un lien entre cette notion d'aire délimitée par une courbe et une autre notion : celle de dérivée.

Considérons une fonction, par exemple la fonction qui à un nombre x associe la grandeur x - x³/3. La valeur de cette fonction en x + h est (x + h) - (x + h)³/3. Un raisonnement algébrique simple montre que la différence entre la valeur de cette fonction en x + h et sa valeur en x est : h - x² h - x h² - h³/3. Le « taux d'accroissement » de la fonction entre x et x + h s'obtient en divisant cette quantité par h ce qui donne 1 - x² - x h - h²/3. Le taux d'accroissement instantané en un point x, la « dérivée » de la fonction en x, s'obtient en observant ce que devient ce taux d'accroissement quand h se rapproche de 0 : les deux derniers termes disparaissent et il reste 1 - x².

Ce raisonnement n'est pas nécessaire pour déterminer la dérivée de la fonction qui, à x, associe x - x³/3. En effet, on peut démontrer que la dérivée d'une somme de deux fonctions est la somme de leurs dérivées. Il suffit donc de déterminer la dérivée de x, d'une part, et celle de -x³/3, de l'autre, et de les ajouter. Ensuite, on peut démontrer que multiplier une fonction par une quantité fixe multiplie sa dérivée par cette même quantité. Ainsi, pour déterminer la dérivée de - x³/3, il suffit de déterminer celle de x³ et de la multiplier par -1/3. Enfin, pour déterminer la dérivée de x et de x³, il suffit de savoir que la dérivée de xⁿ est n x ^{n - 1}. La dérivée de x - x³/3 est donc 1 - x².

Quelle différence y a-t-il entre ces deux manières de calculer la dérivée de x - x³/3 ? Dans la première, nous avons eu besoin d'effectuer un petit raisonnement, certes simple, mais qui nous a demandé de réfléchir. Dans la seconde, en appliquant les règles :
- la dérivée d'une somme est la somme des dérivées,
- multiplier une fonction par une quantité fixe multiplie sa dérivée par cette même quantité,
- la dérivée de xⁿ est n x ^{n - 1}, nous avons obtenu la dérivée de x - x³/3 de manière systématique. Une fois la correction de ces trois règles démontrées, la dérivée d'une fonction peut s'obtenir par un simple calcul. Cet algorithme de calcul de la dérivée d'une fonction ne s'applique pas à des nombres mais à des expressions fonctionnelles. D'ailleurs, il ne s'applique pas à toutes les expressions fonctionnelles, mais uniquement à celles qui peuvent s'obtenir à partir de x et de quantités fixes par addition et multiplication : les polynômes.

Des algorithmes plus généraux s'appliquent à des  langages plus riches comprenant, par exemple, les fonctions exponentiel et logarithme et les fonctions trigonométriques, mais ils ne sont pas d'une nature différente.

La fonction qui, à x, associe 1 - x² est la dérivée de la fonction qui, à x, associe x - x³/3. En retournant la phrase, on dit que la fonction qui, à x, associe x - x³/3 est une « primitive » de celle qui, à x, associe 1 - x2. On peut démontrer que cette fonction a plusieurs primitives toutes obtenues en ajoutant une quantité fixe à celle-ci.

En retournant les règles du calcul de la dérivée, il n'est pas difficile de construire un algorithme qui calcule une primitive d'une fonction :
- une primitive d'une somme de fonctions est la somme des primitives des fonctions ;
- multiplier une fonction par une quantité fixe multiplie une primitive par cette même quantité ; - une primitive de xⁿ est x ^{n + 1}/(n +1).

En appliquant ces règles de manière systématique, on peut calculer une primitive de 1 - x² : x - x³/3.

Revenons au problème des aires : le théorème fondamental du calcul intégral établit un lien entre la notion d'aire et cette notion de primitive. En effet, si on appelle F(x) la fonction qui, à chaque nombre x, associe l'aire de la partie du segment de parabole située à gauche de la verticale d'abscisse x, il n'est pas difficile de montrer que, comme la fonction qui, à x, associe 1 - x² est continue, la dérivée de la fonction F est précisément la fonction qui, à x, associe 1 - x².

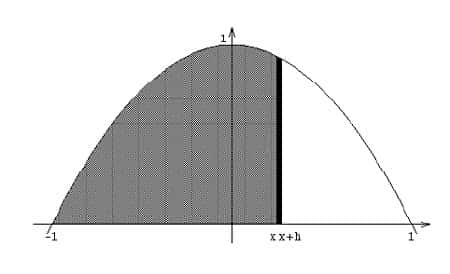
Autrement dit, la fonction F est une primitive de 1 - x² : c'est une fonction qui, à x, associe x - x³/3 plus une valeur fixe. Comme en x = - 1 la fonction F vaut 0, cette valeur fixe ne peut être que 2/3 et F est la fonction qui, à x, associe x - x³/3 + 2/3. L'aire du segment de parabole est la valeur de cette fonction en 1 : 4/3. On aboutit au même résultat qu'Archimède, par une autre méthode que la décomposition du segment de parabole en triangles. Déterminer l'aire du segment de parabole délimité par la courbe y = 1 - x² ne demande donc nullement de construire un raisonnement complexe pour déterminer l'aire de triangles en lesquels ce segment se décompose : il suffit de calculer une primitive de 1 - x² en appliquant l'algorithme précédent, d'ajuster la constante pour que cette primitive vaille 0 en -1 et de prendre sa valeur en 1.

Comme l'algorithme de calcul des dérivées, cet algorithme s'applique uniquement aux polynômes. Des algorithmes plus généraux s'appliquent à des langages plus riches, mais cet algorithme se généralise moins bien que celui de calcul des dérivées. Le calcul de primitives est resté pendant plus de trois siècles un mélange d'algorithmes et de tours de passe-passe pour lesquels une certaine habileté était nécessaire, regardant tantôt du côté du calcul, tantôt du côté du raisonnement. Ce n'est qu'au XXe siècle que la théorie algorithmiquealgorithmique de l'intégration s'est systématisée avec le développement des programmes de calcul formel, dont nous aurons l'occasion de reparler.

Pour revenir au XVIIe siècle, le développement de ces notions de dérivée et de primitive, et les algorithmes qui vont avec, ont permis de réduire à de simples calculs de nombreuses déterminations d'aires, mais aussi de volumes, de longueurs, de centres de gravité... La systématisation de la résolutionrésolution d'un certain  type de problèmes permet de résoudre ces problèmes à moindre coût, donc d'explorer des territoires mathématiques plus vastes. Les mathématiciens de l'Antiquité avaient déterminé les aires de quelques figures, ceux du XVIIe siècle sont allés beaucoup plus loin. Déterminer l'aire délimitée entre -1 et 1 par une courbe compliquée comme celle d'équation y = 2 - x² - x⁸ aurait été un casse-tête pour les mathématiciens de l'Antiquité, mais était un jeu d'enfant pour les mathématiciens du XVIIe siècle, puisqu'il suffit de calculer la primitive de 2 - x² - x⁸ qui s'annule en -1 (2x - x³/3 - x⁹/9 + 14/9) et de prendre sa valeur en 1 : 28/9. De tels outils algorithmiques donnent des forces pour attaquer des problèmes qui paraîtraient démesurés si on devait les attaquer à « mains nues ». Et de nouvelles figures géométriques, dont l'étude aurait été trop difficile sans ces outils, sont apparues au XVIIe siècle.

Cette incursion de méthodes algorithmiques dans la géométrie, c'est-à-dire dans le « Saint des Saints » de la méthode axiomatique, a laissé des traces profondes jusque dans le nom de cette branche des mathématiques. Pour la désigner, on ne parle jamais de « théorie intégrale », mais toujours de « calcul intégral ». En anglais, le mot calculus désigne exclusivement cette branche des mathématiques, et un autre mot, computation, désigne le calcul en général.