au sommaire
Principe bien connu des dessinateurs, la représentation de la perspective doit être maîtrisée pour être parfaitement réussie. C'est ce à quoi s'emploie la géométrie projective, l'étude des projections des objets sur un plan.

Géométrie projective. © 8300 - Domaine public
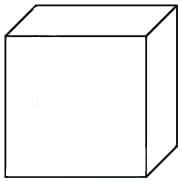
Représentation d'un hexagone au moyen de la perspective. © DR
Quel est cet objet ci-dessus ?
Allez au coin si vous répondez un cube ! Rassurez-vous, vous ne serez pas seul. C'est, bien sûr, un hexagone. Les cubes sont des objets à trois dimensions et leur représentation est à deux dimensions. Nous « voyons » des objets à deux dimensions comme s'ils étaient des volumes. La représentation sur un plan des objets à trois dimensions ne devint une discipline mathématique qu'au milieu du XVIIe siècle.
Les astuces de la perspective
Les artistes italiens de la Renaissance désiraient représenter les merveilles du monde par leur peinture. Un des fondateurs de la géométrie projective, l'étude des projections des objets sur un plan, fut l'artiste et architectearchitecte Leon Battista AlbertiLeon Battista Alberti. La première astuce d'Alberti fut de n'utiliser qu'un œilœil pour peindre. Comme nos yeux sont séparés, chacun voit une image du monde légèrement différente ; le cerveau associe ces deux images pour créer un effet tridimensionnel et la faculté d'évaluer les distances. Quand nous fermons un œil, cette vision stéréoscopique disparaît et notre perception du monde est aplatie. Les films modernes « en relief », c'est-à-dire à trois dimensions, inversent ce processus : les lunettes nous font voir par chaque œil des visions légèrement différentes et notre cerveaucerveau, trompé par cette vision, croit voir des objets à trois dimensions.
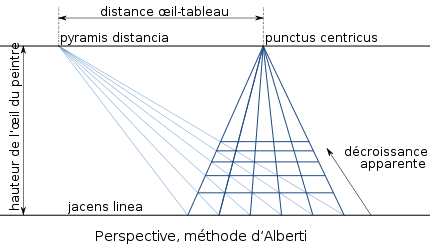
Alberti a donné une belle méthode de construction de la décroissance de la profondeur apparente des carreaux lorsque l'on s'éloigne de la ligne de terre, en perspective. © Coyau licence Creative Commons paternité – partage à l’identique 3.0 (non transposée
La seconde astuce d'Alberti fut de placer une plaque de verre devant le
sujet à peindre. Plaçant sur le verre des marques correspondant à certains points du sujet, Alberti dessinait ensuite la scène sur l'écran en respectant ces marques. Plus tard, il utilisa un quadrillage vertical fait de fils et un quadrillage horizontal identique pour marquer les points repérés sur le quadrillage vertical.
En 1636, le mathématicienmathématicien français Girard Desargues publia un article établissant les méthodes géométriques pour construire des projections. Il analysa mathématiquement la perspective et détermina quels éléments d'une scène se retrouvent sur la projection. Sur une perspective, les points, droites et plans d'une scène sont représentés aussi par des points, des droites et des plans. Au contraire, les angles, les longueurs et les rapports de longueurs changent. La différence la plus notable est la manière dont les parallèles se rencontrent.
Dans une projection plane, toutes les parallèles ne se coupent pas. Celles qui s'éloignent de l'observateur se coupent au « point de fuite ». Les parallèles qui parcourent de droite à gauche notre champ de vision (voir la figure ci-contre) restent parallèles, mais leur espacement diminue quand elles s'approchent du point de fuite, une propriété qu'elles n'ont pas nécessairement dans le monde réel. Prenons un échiquier : comment pouvons-nous le représenter avec exactitude en géométrie projective ? Alberti savait comment faire, comme détaillé ci-contre.