Un des plus grands experts de la théorie des supercordes appliquée aux trous noirs, Juan Maldacena, a trouvé avec un collègue une solution décrivant un trou de ver traversable sans danger pour un humain. Remarquablement, elle émerge d'une variante de la théorie considérée par le prix Nobel Kip Thorne pour rendre crédible scientifiquement le film Interstellar.
au sommaire
En novembre 2015, fut fêté le centenaire de la formulation finale par EinsteinEinstein de sa théorie de la relativité générale. À peine un mois plus tard, on pouvait célébrer l'astronomeastronome et physicienphysicien Karl Schwarzschild qui a publié en janvier 1916 sa fameuse solution décrivant le champ de gravitation d'une étoile sphérique et homogène. Au cours des deux années qui allaient suivre, Einstein, de son côté, découvrait dans sa théorie la possibilité de l'existence d'ondes gravitationnellesondes gravitationnelles et celle de la constructionconstruction d'une véritable cosmologie faisant intervenir une mystérieuse constante.
LigoLigo et VirgoVirgo ont confirmé l'existence des ondes gravitationnelles ; la cosmologie relativiste du Big BangBig Bang a connu un succès éclatant, le tout dernier venant des mesures du rayonnement fossile par le satellite Planck et même, la constante cosmologique d'Einstein semble bel et bien réelle en raison de la découverte de l'accélération de l'expansion de l'Univers observable, peut-être causée par une mystérieuse énergie noire.
La solution de Schwarzschild s'est montrée encore plus étonnante quand bien même son découvreur n'eut malheureusement pas le temps de le comprendre, décédant très peu de temps après sur le front russe au cours de la première guerre mondiale. Karl Schwarzschild n'a en effet rien su des travaux de pionnier en 1939 de Robert Oppenheimer.
Les ponts d'Einstein-Rosen
Grand lecteur de la Bhagavad Gita, le père de la bombe A avait en effet posé à cette occasion et, via deux articles écrits en collaboration avec ses étudiants de l'époque -- On Massive Neutron Cores, avec Georges Volkoff, et On Continued Gravitational Contraction, avec Hartland Snyder --, le socle sur lequel les théories des étoiles à neutrons, et surtout celle de l'effondrementeffondrement gravitationnel conduisant à la formation d'un trou noir, seront construites à la fin des années 1950 et au début des années 1960.
Nous avons toutes les raisons de penser aujourd'hui que les trous noirstrous noirs existent bien comme l'ont à nouveau fortement suggéré les premiers indices de l'existence des modes quasi-normaux des trous noirs et les observations de la collaboration Event Horizon Telescope. On a donc de nouveaux motifs pour prendre au sérieux l'héritage d'Einstein et Schwarzschild, à savoir plus précisément l'existence de trous de ver, selon l'expression de John Wheeler.
Jean-Pierre Luminet nous parle des trous de ver, de leur connexion avec les trous noirs en rotation et du voyage interstellaire. © Jean-Pierre Luminet, YouTube
Là encore, Schwarzschild ne pouvait se douter de ce qu'Einstein et son collaborateur de l'époque, Nathan Rosen, allaient découvrir en 1935 en étudiant sa solution sous un jour nouveau. Au départ, il s'agissait pour Einstein de trouver une solution de ses équationséquations du champ de gravitationgravitation couplées aux équations du champ électromagnétiquechamp électromagnétique de Maxwell, mais dans la version en espace-tempsespace-temps courbes qu'il avait découvert au cours des années 1910. Cette solution promettait d'ouvrir la voie à un traitement des particules de matièrematière purement en terme d'équations de champ et donc de les déduire des équations de la relativité généralerelativité générale, une fois convenablement unifiée avec le champ électromagnétique. L'existence de particules de matière chargées n'était donc potentiellement plus un axiomeaxiome à ajouter aux théories physiquesphysiques mais une conséquence de ces théories. En plus d'ouvrir la voie à une unification des forces, on pavait celle menant peut-être vers une théorie non dualiste de la matière et des champs de forces, voire une nouvelle théorie quantique.
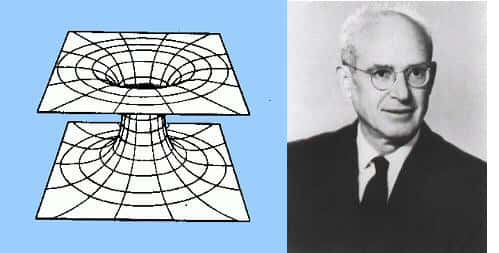
Einstein et Rosen découvrirent donc à cette occasion qu'il y avait une topologie cachée derrière la solution de Schwarzschild que l'on pouvait interpréter, par analogieanalogie avec un modèle de l'espace courbe en deux dimensions comme une sorte de tube reliant deux feuillets d'espace-temps, donc entre deux univers ou, plus certainement dans l'esprit d'Einstein, entre deux régions de l'espace. La théorie des ponts d’Einstein-Rosen était née.
Comme il pouvait servir de raccourci entre deux de ces régions et permettre de contourner l'interdit d'Einstein concernant la vitesse de la lumièrevitesse de la lumière, la science fiction s'est rapidement emparée du concept pour le voyage interstellaire comme l'explique Jean-Pierre LuminetJean-Pierre Luminet dans la vidéo ci-dessus. Malheureusement, on s'est aperçu par la suite que les ponts d'Einstein-Rosen étaient en fait dynamiques et pas traversables. Un voyageur imprudent y pénétrant verrait la géométrie de l'espace-temps changer au point de finir par l'écraser en un point singulier de cet espace-temps.

On est donc quelque peu fasciné, même s'il faut garder la tête froide à ce stade, par un récent article déposé sur arXiv par Juan Maldacena et Alexey Milekhin. Maldacena s'est fait un nom au milieu des années 1990 au moment où la seconde révolution des supercordes était en cours. Ses travaux sur l'entropieentropie des trous noirs dans le cadre de la théorie des cordesthéorie des cordes l'ont conduit à formuler la fameuse correspondance AdS/Cft étendant les travaux de Susskind et 't Hooft sur le principe holographique avec la théorie des trous noirs et ses implications pour le fameux paradoxe de l’information découvert par Stephen HawkingStephen Hawking.
Les trous de ver de Contact à Interstellar
Maldacena et Milekhin annoncent que, selon eux, il existe une solution décrivant des trous de ver traversables par des êtres humains et ce, dans le cadre d'un modèle d'une nouvelle physique construite à partir du célèbre modèle cosmologique de Randall-Sundrum II. On en vient tout de suite à penser, et par un détour très étonnant en plus, que la science-fiction s'est rapprochée un petit peu plus de la réalité avec la question du voyage interstellaire avec un trou de ver.

Rappelons que c'est en 1988 que le prix Nobel de physique Kip Thorne avait stupéfié le monde de la physique en publiant avec ses collègues Michael S. Morris et Ulvi Yurtsever un article démontrant que, non seulement les équations d'Einstein possédaient une solution décrivant un trou de ver traversable, mais aussi qu'il permettait de voyager dans le temps. La découverte s'était faite alors que Thorne cherchait à rendre crédible, à la demande de Carl Sagan, l'existence d'un tel objet pour son célèbre roman de science-fiction, Contact.
Thorne allait reprendre l'idée pour sa collaboration en tant que conseiller scientifique du film du réalisateur britannique Christopher Nolan, Interstellar. Futura avait longuement commenté la science derrière Interstellar et avait expliqué qu'elle faisait justement intervenir une solution décrivant un trou de ver dans une version de la théorie de Randall-Sundrum comme on peut le voir en détails avec le précédent article ci-dessous.
Rappelons brièvement que, dans les deux modèles proposés par LisaLisa Randall et Raman Sundrum, l'espace-temps est à 5 dimensions et que notre Univers observable est une sorte de feuillet d'espace-temps à 4 dimensions connecté à un second feuillet, lui aussi, à 4 dimensions et donc la distance à notre « membrane » est faible selon la cinquième dans le cas du modèle I et infinie dans le cas de la seconde, le modèle II. Ces deux modèles permettaient de penser que la fameuse massemasse de PlanckPlanck ordinairement conçue comme phénoménalement élevée pouvait être suffisamment basse pour que l'on puisse créer des minitrous noirs au LHCLHC. Il n'en a rien été.
Un voyage de dizaines de milliers d'années-lumière en une seconde
Maldacena et Milekhin se sont donc penchés sur la question de l'existence de trou de ver traversable par une personne de taille humaine dans le cadre du modèle RSII. Ils annoncent donc aujourd'hui qu'une telle solution devrait bel et bien exister si l'on suppose, en plus de l'espace-temps, l'existence de certaines particules et l'équivalent du champ électromagnétique mais ne manifestant leur présence vis-à-vis des particules du Modèle standardModèle standard que par leur gravitégravité (un secteur « sombre » dans le jargon des physiciens). Il apparaît alors une énergieénergie exotiqueexotique qui serait négative dans la solution trou de ver, précisément ce qui le rend traversable en créant une pressionpression s'opposant à la contraction de la gorge du trou de ver pour une personne ou un objet cherchant à le traverser, exactement comme dans le cas considéré par Thorne et ses collègues en 1988.
Une interview de Juan Maldacena. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © Breakthrough
La solution trou de ver ainsi identifiée se comporte comme si ses deux entrées apparaissaient comme des trous noirs extrêmes mais magnétiquement chargés.
Il existe une solution des équations d'Einstein-Maxwell décrivant un trou noir avec une charge électrique et sans rotation. Il s'agit de la solution découverte indépendamment et avant 1920 par Hans Reissner et Gunnar Nordström (qui eux non plus n'avaient aucune idée qu'il s'agissait d'un trou noir). Une généralisation existe portant une charge magnétique mais comme nous n'avons toujours pas découvert de monopôle magnétiquemonopôle magnétique, elle n'est considérée que dans des études spéculatives. Dans les deux cas, le trou noir est dit extrême quand la charge a une valeur maximale pour une masse donnée associée au trou noir -- au delà, la singularité centrale du trou noir n'est plus cachée par un horizon des événementshorizon des événements, ce qui est très problématique et semble réfuter l'existence de la solution.
Toujours est-il que, d'après les calculs de Maldacena et Milekhin, la solution qu'ils ont trouvée permet bien de faire passer un humain en bon état en une seconde d'un point à un autre de la Voie lactéeVoie lactée, séparé par une distance de plusieurs dizaines de milliers d'années-lumièreannées-lumière mais une fois entré dans le trou de ver, il sortirait aussi plusieurs dizaines de milliers d'années plus tard. Autre problème, des photonsphotons ou des particules entrant dans le trou de ver subiraient une forte accélération (enfin pour un photon il faut parler d'un apport important d'énergie et pas d'accélération), ce qui pourraient les rendre dangereuses pour un humain dans le trou de ver et surtout conduire à une composante d'énergie positive annulant l'énergie négative maintenant le trou ouvert. Il faudrait donc que le trou de ver se trouve dans un milieu très froid, plus que le rayonnement fossilerayonnement fossile à 3 K.
Les chercheurs précisent aussi qu'ils ne savent pas comment il faudrait s'y prendre pour créer un tel trou de ver traversable mais peut-être qu'en poursuivant leurs recherches -- qui sont encore peu développées et uniquement dans un article qui n'a pas encore passé le filtre de la relecture par d'autres experts pour publication --, une perspective nettement plus enthousiasmante émergera comme dans Interstellar avec les travaux de Murphy Cooper. On verra...
Interstellar et les secrets de la physique des trous de ver
Article de Laurent SaccoLaurent Sacco publié le 15/11/2014
Comme nous l'expliquions dans un précédent article, le dernier film du réalisateur britannique Christopher Nolan, Interstellar, contient de nombreuses références à la physique et à l'astrophysiqueastrophysique des trous noirs. C'est vers ces objets étranges que sont les trous de ver que nous nous tournons maintenant. Leurs propriétés, toujours théoriques car nous n'avons encore aucune preuve de leur existence, sont en effet au cœur du scénario d'Interstellar.
Interstellar ne repose pas seulement sur la physique des trous noirs mais aussi sur celle des trous de ver que l'on désigne en anglais par wormholes. C'est le grand physicien John Wheeler qui a introduit cette dénomination en 1957, dix ans avant celle de trou noir dont il est aussi à l'origine. Tout comme un tunnel creusé par un ver dans une pomme constitue un raccourci entre deux points sur la surface de cette pomme, un wormhole est un pont entre deux régions de l'espace-temps permettant en théorie de se rendre de l'une à l'autre dans un temps plus court, voire de voyager dans le temps.
Des ponts d'Einstein-Rosen aux trous de ver de Thorne-Morris
Albert Einstein et Nathan Rosen ont découvert pour la première fois en 1935 que les équations de la théorie de la relativité générale possédaient des solutions de ce type. Le pont d'Einstein-Rosen, comme on l'appelle désormais, était implicitement contenu dans la métrique de Schwarzschild dont on a réalisé plus tard qu'elle décrivait aussi les trous noirs sans rotation et sans charge électrique ou magnétique. Mais le pont d'Einstein-Rosen ne décrivait pas vraiment un raccourci entre deux régions de l'univers mais bien plutôt entre deux univers parallèles. C'est Charles Misner qui a découvert une solution permettant d'imaginer se rendre du Système solaireSystème solaire à Alpha et Proxima du Centaure en un temps plus court que celui que mettrait la lumière pour voyager du SoleilSoleil à l'une de ces étoiles. Hélas, tout comme dans le cas du pont d'Einstein-Rosen, les traverser se révèle impossible quand on étudie de plus près les prédictions des équations d'Einstein gouvernant la courbure de l'espace et du temps.
Mais au milieu des années 1980, le grand astrophysicienastrophysicien relativiste Kip Thorne, qui fut conseiller scientifique d'Interstellar, s'est finalement rendu compte qu'il existait des trous de ver traversables pourvu que l'on puisse disposer de ce que l'on appelle de la matière ou de l'énergie exotique. Certains états du vide quantique que l'on peut obtenir par effet Casimireffet Casimir ressemblent à ceux de cette matière exotique, mais il n'en existe pour le moment aucune trace dans l'univers. En tout état de cause, les premiers calculs concernant la quantité d'énergie nécessaire pour ouvrir un trou de ver traversable indiquent qu'il faudrait disposer de bien plus de celle qui est émise par une étoile comme le Soleil en une année.
En réalité, la question du moyen pour ouvrir un trou de ver traversable et de la quantité d'énergie dont il faudrait disposer reste sans réponse nette. La raison en est double. Personne ne sait vraiment si la théorie de la relativité générale d'Einstein est toujours valide dans les régions de fortes courbures de l'espace-temps comme celles régnant à l'intérieur d'un trou noir ou dans un trou de ver en formation. Enfin, les singularités de l'espace-temps que l'on sait exister au cœur des solutions décrivant ces objets dans le cadre de la théorie de la relativité générale classique sont probablement inexistantes lorsque la mécanique quantiquemécanique quantique entre en ligne de compte. Seule une théorie complète de la gravitation quantiquegravitation quantique pourrait permettre de répondre à la question de savoir si l'on peut voyager bien plus vite que la lumière dans l'univers avec des trous de ver.
De fait, à la fin des années 1990, un grand espoir était né au sein de la communauté des physiciens théoriciens. L'existence de dimensions spatiales supplémentaires, en particulier dans la théorie des supercordesthéorie des supercordes, permettait d'imaginer que l'énergie nécessaire pour créer des trous noirs, et donc aussi des trous de ver en laboratoire, par des processus de gravité quantique pouvait être bien plus faible que ce que l'on croyait jusque là, à savoir la mythique masse de Planck valant 1016 TeV. Au lieu de requérir un accélérateur de particules de la taille de la Voie lactée, dont le diamètre est de 100.000 années-lumière, il pouvait suffire du LHC avec ses énergies de l'ordre de 10 TeV.

Des trous de ver dans la cosmologie de Randall-Sundrum
Dans Interstellar, il est question, à plusieurs occasions, d'un espace-temps à 5 dimensions, d'un mystérieux « Bulk » et de gravité quantique régnant à l'intérieur d'un trou noir. Toutes ces références s'éclairent lorsque l'on connaît l'existence de l'une des théories avec des dimensions spatiales supplémentaires proposée à la fin des années 1990, celle de Lisa Randall et Raman Sundrum. Elle se décline en deux versions mais elles ont en commun de supposer que notre univers en 4D est une sorte de membrane plongée dans un espace-temps en 5D que l'on appelle précisément le « Bulk » un mot anglais signifiant volumevolume ou vrac. Par analogie, on peut s'imaginer notre univers comme une feuille 2D flottant dans l'espace. Un trou noir est donc une région dont la lumière ne peut s'échapper, caractérisée par un horizon des événements qui y serait représenté par un cercle et les trous de ver par un tube connectant deux régions similaires de forme circulaire. Comme le montre Interstellar, un trou de ver nous apparaîtrait donc comme une sphère d'où émergeraient les rayons lumineux en provenance du reste de l'univers plongeant dans l'autre extrémité du trou de ver.
Dans le cadre d'un modèle cosmologique de Randall-Sundrum (RS), on peut imaginer créer des minitrous noirs au LHC, et peut-être donc aussi des trous de ver. On les a cherché, jusqu'ici sans résultats et il semble maintenant probable que l'on n'en trouvera pas pour plusieurs raisons. Si nous vivons dans un univers de type RS, il doit exister un mécanisme qui explique pourquoi la matière et la lumière ne semblent apparemment pas pouvoir voyager dans une quatrième dimension spatiale. La théorie des supercordes fournit un tel mécanisme qui « colle » en quelque sorte les particules du modèle standard sur la membrane dans laquelle nous serions... à l'exception des gravitons. Comme il est dit dans le film de Christopher Nolan, seule la gravité peut se propager dans l'espace-temps complet à 5D. Mais rien n'empêche d'imaginer des êtres intelligents nés dans le Bulk qui n'auraient pas ces limites.
L'idée est ancienne puisqu'on la trouve dans Flatland, une allégorie écrite en 1884 par Edwin Abbott Abbott et reprise dans le cadre de la physique moderne par le mathématicienmathématicien Rudy Rucker dans The Fourth Dimension: A Guided Tour of the Higher Universes. Abbott et Rucker y essayaient d'imaginer comment serait l'existence dans un monde avec quatre dimensions spatiales et comment des êtres y existant se manifesteraient pour nous en s'aidant de l'analogie constituée par des êtres vivants dans un monde en 2D, Flatland, confronté à des êtres vivants en 3D. Un exemple d'une telle manifestation pour des êtres en 2D serait la brutale apparition d'objets ou d'effets semblant venir de nulle part puisque, effectivement, ils viendraient de l'espace 3D. C'est précisément ce que l'on peut voir dans Interstellar. Une autre manifestation spectaculaire serait qu'un être enfermé dans une pièce 2D pourrait s'en échapper si un être 3D le décollait de Flatland pour le « recoller » à l'extérieur de la pièce ou s'il existait un trou de ver connectant l'intérieur de cette pièce à une autre région de Flatland.
La transposition de toutes ces considérations à Interstellar est donc évidente. Kip Thorne a supposé que nous vivions bien dans un univers décrit par un modèle cosmologique de type RS et qu'une mystérieuse civilisation avancée maîtrisant les lois de la gravitation quantique y utilise les possibilités offertes par un modèle RS avec une masse de Planck basse pour créer des trous de ver ou influencer des régions de l'espace-temps, à l'aide de la gravité. L'un des enjeux de l'humanité dans le film de Nolan est donc d'arriver elle aussi à la connaissance et à la maîtrise des lois de la gravitation quantique
Les trous de ver, des machines spatiotemporelles
Il existe une question profonde que soulève la physique des trous de ver et qui est aussi abordée dans Interstellar. Comme Kip Thorne l'a montré en 1988 avec son étudiant de thèse de l'époque Michael Morris, des trous de ver traversables autorisent en principe des voyages dans le temps. Cela ouvre bien sûr la porteporte à toute sorte de paradoxes concernant la causalité comme celui du grand-père de Barjavel. Mais comme l'a montré un collègue de Kip Thorne, Igor Novikov, rien dans les lois de la physique n'exclut l'existence de boucles causales autocohérentes dans l'espace-temps. Si la logique semble exclure la possibilité que vous remontiez dans le temps pour vous empêcher de construire la machine spatiotemporelle qui vous permettra d'effectuer ce voyage, rien ne semble pouvoir vous empêcher de remonter dans le temps pour vous expliquer à vous-même comment s'y prendre pour construire une telle machine.
Existe-t-il des trous de ver naturels dans l'univers ? Probablement à des échelles de distances bien inférieures celles des protonsprotons et des neutrons du fait des fluctuations quantiques de l'espace-temps. Mais il se pourrait que les conditions physiques bien particulières ayant régné dans l'univers primordial, notamment pendant une phase d'inflation, aient conduit à la formation de trous de ver aujourd'hui macroscopiques. Certains trous noirs supermassifs, comme celui baptisé Gargantua dans Interstellar, pourraient être en fait des trous de ver fossiles menant à d'autres régions du cosmoscosmos et peut-être à des univers parallèles. On va essayer de vérifier cette théorie avec RadioAstron.
Ce qu’il faut
retenir
- Un des plus grands experts de la théorie des supercordes appliquée aux trous noirs, Juan Maldacena, a trouvé avec un collègue une solution décrivant un trou de ver traversable sans danger pour un humain.
- Remarquablement, elle émerge d'une variante de la théorie considérée par le prix Nobel Kip Thorne pour rendre crédible scientifiquement le film Interstellar.
- Un tel trou de ver permettrait à un voyageur de passer d'un point à un autre de la Voie lactée en quelques secondes tout au plus mais, pour des observateurs extérieurs, le voyageur émergerait de l'autre bout du trou de ver des dizaines de milliers d'années après y être entré.
- On ne sait pas comment créer ce type de trou de ver qui est parent de ce que serait un trou noir magnétiquement chargé mais peut-être l'avenir nous donnera-t-il bientôt la réponse.
























