au sommaire
Le résultat théorique établi par Shannon a constitué pour des milliers de chercheurs et d'ingénieurs un défi scientifique majeur car l'enjeu économique est considérable.

Améliorer le pouvoir de correction d'un code, c'est, à même qualité d'information reçue (par exemple, pas plus d'une information binairebinaire fausse sur 10.000 reçues en téléphonie numériquenumérique), permettre au système de transmission de fonctionner dans des conditions plus sévères.
Il est alors possible de réduire la taille des antennes, le poids des batteries d'alimentation ou l'encombrement des panneaux solaires. Dans les systèmes spatiaux (satellites, sondes...)), l'économie peut se chiffrer en dizaines de millions de dollars, car le poids des équipements et la puissance du lanceur s'en trouvent notablement réduits.
Codage convolutif
Le codagecodage correcteur d'erreurs a été, jusqu'à ces dernières années, une affaire plutôt américaine. Une contribution majeure fut celle de Peter Elias qui introduisit le codage convolutif (1954), c'est-à-dire l'art et la manière de rendre un message binaire redondant de façon subtile. Le plus simple des procédés de codage consisterait à transmettre deux fois le même message, mais cela ne permet pas de corriger les erreurs ; cela les détecte simplement.
Supposons par exemple que l'on veuille transmettre « matin » et qu'après la double transmission, le récepteur comprenne la première fois « matin » et l'autre fois « satin ». Il y a de toute évidence une erreur quelque part, mais est-ce « matin » ou « satin » que le récepteur doit retenir ? Un codage plus élaboré consiste à transmettre le message original accompagné d'un synonyme : « matin » et « aube » par exemple. Si l'on reçoit « tatin » et « aube », ou « matin » et « auge », la correction est possible. C'est cette constructionconstruction de synonymes, sous une forme binaire, que réalise le codage convolutif (illustration 2 ci-dessous).
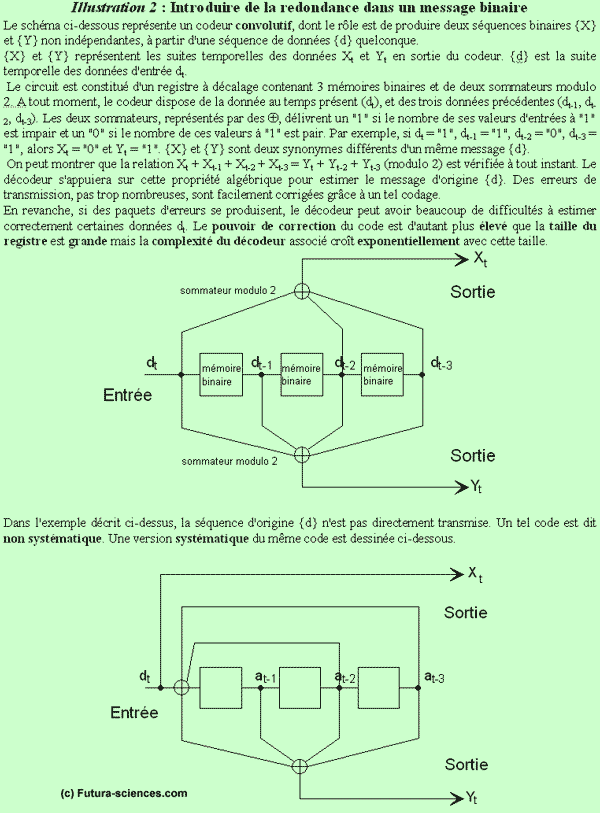
Limite de Shannon
Bien sûr, si de nombreuses erreurs altèrent la transmission et si l'on reçoit « lapin » et « cube », on n'y comprendra plus rien. Il existe ainsi une limite au pouvoir de correction. C'est la fameuse limite de Shannon, qu'aucun code correcteur ne pourra, en théorie, dépasser. Pour un taux de redondance rajoutée de 100 % (c'est-à-dire deux fois plus de données transmises que n'en contient le message d'origine), cette limite correspond précisément à la situation où la puissance moyenne de la perturbation est égale à la puissance moyenne du signal utile reçu.
L'illustration 3 (ci-dessous) représente une telle dégradation. À gauche, dans le plan amplitude-phase, ou plan de Fresnel, les deux petits cercles correspondent à ce que l'on devrait recevoir idéalement : +A pour un « 1 » logique, -A pour un « 0 » logique. Dans la partie droite, au signal utile, se rajoute un bruit de même puissance. Le point reçu occupe alors une position aléatoire dans le plan x-y, autour des points +A ou -A. L'illustration représente un ensemble de positions observées dans le récepteur pour plusieurs valeurs binaires transmises.
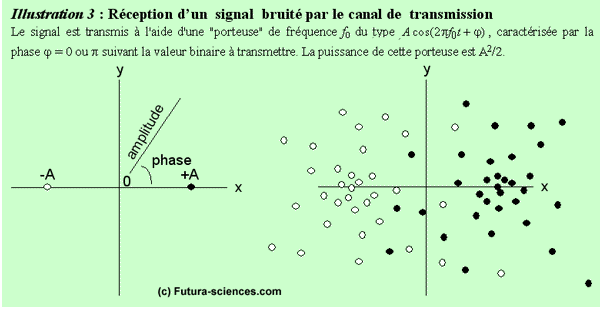
À droite, il y a erreur de transmission chaque fois qu'un petit cercle plein est détecté dans le demi-plan gauche, ou qu'un cercle vide est détecté dans le demi-plan droit. Lorsque les puissances de signal et de bruit sont égales, cela conduit en moyenne à une information binaire erronée sur douze, ce qui donne un taux d'erreurstaux d'erreurs très élevé. En considérant, par exemple, un texte dont les caractères (minuscules, majuscules, ponctuation, etc.) sont codés sur 6 valeurs binaires, un tel taux d'erreurs, s'il n'y avait pas de code correcteur, mettrait en défaut 2 caractères sur 5 en moyenne (6 valeurs binaires permettent de distinguer 26 = 64 caractères, si la probabilité d'erreur sur une valeur binaire est p = 1/12, la probabilité d'erreur sur le caractère est 1 - (1-p)6 soit environ 0,4) !



























