Le surbooking : comment ça marche ?

Le surbooking nous semble une pratique détestable quand nous en sommes victimes. Certains tribunaux l’estiment même frauduleuse. Elle fait pourtant aujourd’hui partie des habitudes de gestion des compagnies aériennes et s’étend progressivement à d’autres moyens de transport, à des agences de voyages et même à certains hôtels. Pourquoi est-elle pratiquée alors qu’elle peut nuire à l’image de marque des compagnies aériennes et déboucher au versement d’indemnités importantes ?

Comment s’explique le surbooking ? © ThePixelman, Pixabay, DP

Réponse 

Les compagnies aériennes vendent plus de billets qu’il y a de places dans les avions car, statistiquement, un certain pourcentage des passagers ne se présentent pas à l’embarquement du vol sur lequel ils ont réservé. Bien sûr, ce sont plutôt les passagers qui ont des billets remboursables qui ne se présentent mais, pour simplifier, nous estimerons qu’ils sont tous égaux et indépendants.

Le calcul des compagnies aériennes

Prenons l’exemple d’une compagnie aérienne qui, par une méthode statistique, estime que chaque passager a une probabilité de 90 % de se présenter effectivement à l’embarquement. Imaginons qu’elle vende 106 billets sur un vol qui ne peut en contenir que 100. Quel est le risque qu’un passager ne puisse pas monter à bord ? La probabilité que les 106 passagers se présentent tous est de 0,9¹⁰⁶, soit environ 1, 5 pour 100.000. On évalue de même la probabilité que 105 passagers se présentent (106 x 0,9¹⁰⁵ x 0,1), etc. En ajoutant les probabilités de présence de 101 à 106 personnes, on obtient un risque de devoir refuser un passager égal à 4 %. Dans ce cas, la compagnie aérienne doit dédommager le passager mais le jeu en vaut la chandelle ! Qui refuserait de jouer quand la probabilité de gagner est de 96 % ?

Probabilités de remplissage

À partir de ces données, on peut évaluer la probabilité que l’avion soit rempli à 100 %, 99 %, etc. À chaque remplissage correspondent une probabilité et un coût. Il est donc possible d’évaluer une espérance de ce coût. Par exemple, si une perte de 5.000 € est associée à une éventualité de 4 % et un gain de 1.000 € à une éventualité de 96 %, l’espérance de gain est de 0,96 x 1.000 – 0,04 x 5.000, soit 760 €. Le calcul des compagnies aériennes est plus compliqué mais de ce type. En effet, chaque type de passagers a sa probabilité propre de ne pas se présenter. Dans tous les cas, le calcul se justifie par la loi des grands nombres. Plus le nombre de vols de la compagnie est important, plus on se rapproche de ces prévisions.

Nombre optimal de places à vendre

Le problème essentiel est donc d’évaluer correctement le nombre de places à vendre sur chaque vol. Chaque place vide a un coût. Chaque passager devant être refusé en a un autre, double du premier environ. Il est impossible de prévoir exactement le nombre de passagers qui ne se présenteront pas mais, comme nous venons de le voir, on peut estimer les probabilités qu’il en manque un, deux, trois, etc. Selon le surbooking appliqué, nous pouvons en déduire une espérance du nombre de sièges vides et donc celle des personnes non embarquées.

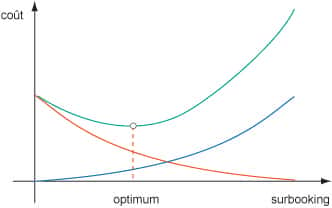
L’espérance du coût est proportionnelle à la somme de l’espérance du nombre de sièges vides plus le double de l’espérance du nombre de sièges indisponibles. On connaît le coût d’un siège vide. On connaît donc les probabilités de coût selon le surbooking effectué. On en déduit une espérance de coût dans chaque cas, ce qui donne deux courbes. Dans tous les cas, il existe un remplissage optimum des avions. Celui-ci n’est pas de 100 % mais plutôt de 115 % environ. Les condamnations par des tribunaux n’y feront rien car elles ne peuvent qu’être intégrées dans les coûts à prévoir en cas de passagers refusés à l’embarquement. Le surbooking est une fatalité. Pour le passager avec un billet non remboursable, le mieux est d’arriver en avance.