Qu’est-ce que le théorème du moustique ?

Avant la découverte de RossRoss, le lien entre les marécages et le paludisme était connu comme le montre les tentatives de drainagedrainage des marais Pontins près de Rome, de l'Antiquité jusqu'au XIX^e siècle. De même, le paludismepaludisme a disparu de France, où il était autrefois endémiqueendémique dans les régions humides comme la Sologne, le marais Poitevin et même autour de Port-Royal des Champs, au cours du XIX^e siècle grâce au drainage ; et non à la consommation de Quinquina, un apéritif à base de QuinineQuinine, préventif du paludisme, comme cela a été parfois affirmé !

Le modèle SIR

Ce théorème a été justifié en 1927 par la première modélisation réaliste du développement des épidémiesépidémies, due à William Kermack (1898 - 1970) et Anderson McKendrick (1876 - 1943). Leur modèle compartimente la population en trois classes : S, la classe des individus susceptibles d'attraper la maladie, I, celle de ceux qui en sont infectés (et contagieuxcontagieux) et R, ceux qui en sont revenus ou morts.

Régions du monde où le paludisme est endémique. © Percherie, Wikimedia Commons, CC by-sa 3.0

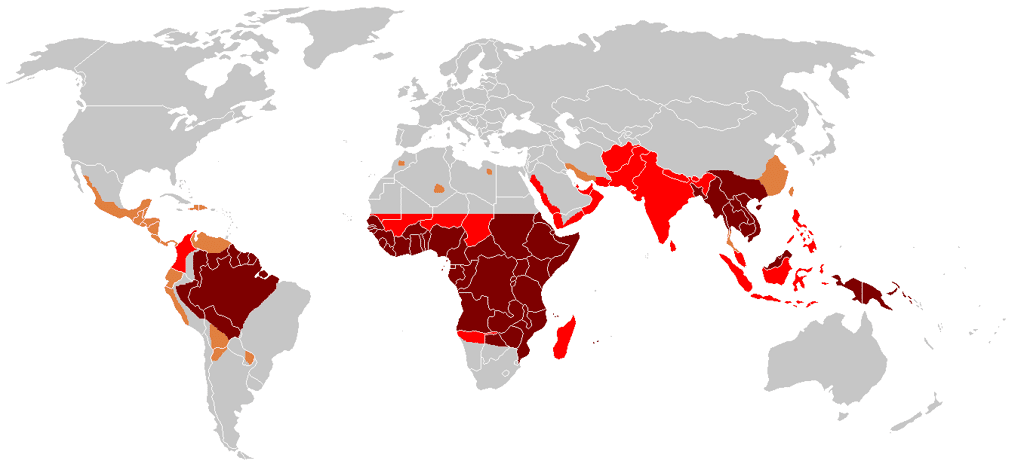
Le modèle SIR suppose implicitement que la population totale n'augmente pas et il considère l'évolution de ces trois classes dans le temps en fonction de deux taux mesurables expérimentalement. Le premier (α) est le taux de contagion de la maladie pour un infecté, c'est-à-dire la probabilité pour qu'un individu susceptible attrape la maladie après contact avec un individu infecté. Le second taux (β) mesure le passage de l'état I à l'état R. Après un laps de temps t, on compte a I S t infectés supplémentaires et R augmente de β  I t. La variation du nombre d'infectés est donc égale à α S - β multiplié par I t.

La condition pour que la maladie se propage (et donc donne lieu à une épidémie) est que le nombre de malades infectés augmente, c'est-à-dire que : α  S - β > 0. Le quotient b / α a donc valeur de seuil. Si le nombre de sujets susceptibles est strictement inférieur à ce seuil, la maladie ne s'étend pas. Sinon, elle donne lieu à une épidémie. En particulier, ce modèle justifie le théorème du moustiquemoustique.