Le nom de Srinivasa Ramanujan est malheureusement peu connu. Cet autodidacte indien a pourtant révolutionné les mathématiques. Pour beaucoup de scientifiques, il est d'ailleurs considéré comme un véritable génie.
au sommaire
AutomneAutomne 1917. Le mathématicienmathématicien Godfrey Harold Hardy, du Trinity College de Cambridge, rend visite à son ami et collègue Srinivasa RamanujanSrinivasa Ramanujan. « Vous êtes venu en voiturevoiture, aujourd'hui, professeur ? », fait-il d'une voix affaiblie par la maladie. « Un taxi », répond Hardy en prenant une chaise. « Le numéro 1729. Mais je doute qu'il s'agisse là d'un nombre intéressant. J'espère que ce n'est pas mauvais signe ! », ajoute-t-il en riant. « Au contraire », répond le malade au bout de quelques secondes. « C'est un nombre extrêmement intéressant. C'est le plus petit nombre décomposable en somme de deux cubes de deux manières différentes. 1729 est égal à 93+103 mais également à 13+123. Voilà une étonnante propriété qu'il faudrait développer ! Nous pourrions le définir comme... un nombre taxicab ! », ajoute Ramanujan en se retournant vers lui et en souriant. Hardy regarde avec affection le jeune prodige des mathématiques. Assurément, il a en face de lui l'un des mathématiciens les plus brillants de l'histoire.
Srinivasa Ramanujan naît le 22 décembre 1887 à Erode, dans le sud de l'Inde. Il est l'aîné de plusieurs frères et sœurs, mais seuls deux survivront aux maladies touchant alors fréquemment les jeunes enfants. D'ailleurs, il contractera lui-même la variolevariole à l'âge de 2 ans, une maladie qui lui laissera des cicatricescicatrices indélébiles et une santé fragile.

À l'école primaire, il devient très rapidement un élève brillant dans tous les domaines. Mais c'est vers l'âge de 10 ans qu'il va développer une subite passion pour une matière bien précise. Une passion si puissante qu'elle gouvernera dès lors le reste de sa vie.
Une obsession des mathématiques dès l’enfance
C'est alors qu'il entre dans l'enseignement secondaire qu'il découvre en effet les mathématiques abstraites. Srinivasa se rend vite compte que, pour lui, les chiffres représentent quelque chose de bien différent que pour les autres élèves. Ils dansent dans sa tête, virevoltent et s'agencent pour lui dévoiler sans effort la solution des équations ou des problèmes. Il s'émerveille d'ailleurs de voir les possibilités presque infinies de raisonnements logiques que permet leur manipulation.
Cet amour des mathématiques va ainsi rapidement tourner à l'obsession. À ces heures perdues, il s'amuse à résoudre des équations de plus en plus complexes. Les cours dispensés à l'école le laissent ainsi bien vite sur sa faim. Il réussit alors à se procurer un premier livre de géométrie qu'il dévore littéralement. À seulement 13 ans, il maîtrise l'ensemble des notions abordées dans le livre et commence à chercher les solutions mathématiques à certaines questions qu'il se pose. Sans le savoir, il redécouvre ainsi par lui-même plusieurs théorèmes déjà énoncés par de grands mathématiciens, mais dont il n'a pas encore la connaissance.
Lorsqu'il entre au lycée, il emprunte un nouveau livre qui va définitivement le positionner sur les rails de la recherche en mathématiques fondamentales, mais d'une façon totalement non conventionnelle. Il se plonge ainsi dans la lecture de l'ouvrage de George Shoobridge Carr, qui contient des milliers de théorèmes et formules, mais très peu de démonstrations. Cette présentation aseptisée et peu rigoureuse de présenter des résultats mathématiques impactera durablement le stylestyle de Srinivasa Ramanujan, un défaut qui lui sera souvent reproché par la suite. De plus, l'ouvrage a été rédigé en 1886 et repose essentiellement sur des notions acquises au début du XIXe siècle. Les mathématiques qu'il présente sont donc certes justes, mais largement dépassées au moment où le jeune mathématicien en herbe s'intéresse de près au contenu du livre. Cet ouvrage jouera cependant un rôle majeur dans la carrière du jeune homme, qui en retire, de façon totalement indépendante, des connaissances de plus en plus poussées en mathématiques.
Un pur autodidacte
En 1904, le jeune homme obtient son diplôme, avec une mention spéciale en mathématiques. Fort de ses excellents résultats scolaires, et sur recommandation du directeur de l'école, il obtient ainsi une bourse d'étude pour entrer au Governement College de Kumbakonam. Mais son temps est de plus en plus exclusivement dédié aux mathématiques, au détriment des autres matières. S'il excelle, et de loin, dans sa discipline favorite, il est en échec total dans toutes les autres matières. Il échoue ainsi aux examens de fin d'année et perd sa bourse d'étude.
Quittant le domicile familial, il décide de tenter une nouvelle école d'enseignement supérieur à Madras, avec l'objectif d'entrer par la suite à l'université. En 1906, alors sans le sou, il intègre ainsi le Pachaiyappa's College de la capitale du Tamil Nadu. Dans l'intervalle, il n'a cependant pas été inactif. Alors qu'il intègre la première année de l'école, il est alors accaparé par l'étude des séries hypergéométriques et se lance sur la piste des relations entre les intégrales et les séries. Il ne le sait pas encore, mais il est en train d'étudier ce que l'on appelle aujourd'hui les fonctions elliptiques. Pur autodidacte, il développe un système de pensée et de notation qui lui sont totalement propres, fonctionnant principalement par intuition et laissant libre cours à sa créativité. Ses travaux, qu'il consigne minutieusement dans ses carnets, ne comportent en général aucune démonstration, ou tout au plus quelques esquisses qui sont, d'un point de vue académique, totalement non conventionnelles. Il effectue ses raisonnements de tête ou sur une ardoiseardoise, ne notant que le résultat final, à l'image du livre de Carr, qui lui sert alors de référence en la matière.
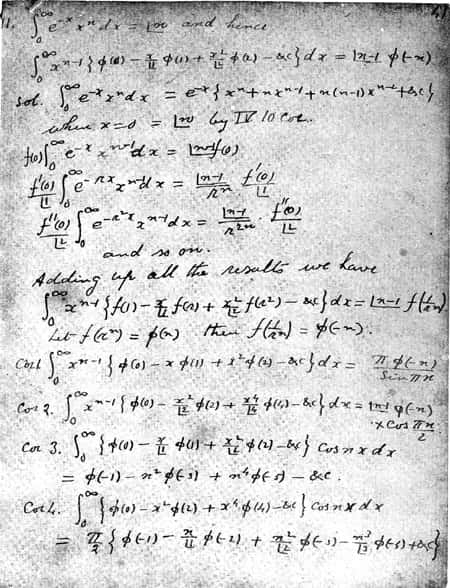
Le jeune homme tombe cependant malade au bout de quelques mois. Trop faible pour continuer sa scolarité, il se présente tout de même à l'examen final mais échoue dans toutes les matières, sauf en mathématiques, naturellement. À son grand désarroi, il n'est pas autorisé à entrer à l'université. Il retentera l'année suivante, pour le même résultat. Dépité, il décide alors d'abandonner l'idée de suivre un cursus académique et poursuit ses travaux en solitaire et sans avoir connaissance des nouvelles théories.
Naissance d’un génie des mathématiques
En 1910, Ramanujan, qui cherche désespérément un emploi afin de subvenir à ses besoins les plus simples, décide d'approcher le secrétaire de la Société indienne de mathématique, Ramachandra Rao. Impressionné par les résultats que lui présente Ramanujan, Ramachandra reste cependant sceptique sur leur authenticité. Mais un entretien plus approfondi lui fait rapidement entrevoir qu'il se trouve en face d'un étonnant et exceptionnel génie en mathématiques. Grâce à sa personnalité calme et douce, Ramanujan s'attire rapidement la sympathiesympathie du mathématicien, qui décide de l'aider.
Grâce au soutien et à l'aide de plusieurs membres de la Société indienne de mathématique, Ramanujan publie ainsi son premier article dans un journal scientifique, bien que n'ayant aucune formation académique ni aucun poste à l'université. Un an plus tard, il propose également une brillante étude sur les nombres de Bernoulli. L'éditeur du journal, s'il reconnaît la valeur et l'originalité des résultats obtenus, regrette cependant le style laconique et la présentation imprécise de l'article, qui rendent son contenu inaccessible à un mathématicien ordinaire. Malgré cela, ses résultats commencent à soulever l'intérêt des universitaires de Madras, qui reconnaissent volontiers le talent exceptionnel du jeune homme.
C'est le cas également du professeur Hardy, du Trinity College de Cambridge, à qui Ramanujan a fait parvenir une partie de ses travaux.
Séjour à Cambridge : le début de la reconnaissance internationale
En ouvrant la lettre de neuf pages sur laquelle s'enchaînent les équations, formules et théorèmes, dans le désordre et avec très peu d'explications, Hardy croit d'abord à une farce. Mais en y regardant de plus près, il reconnaît bien certaines formules. D'autres, en revanche, le laissent perplexe. Intrigué, il tente de vérifier les équations, qui ne ressemblent à rien qu'il ait déjà vu, de près ou de loin, mais n'y parvient pas totalement. « Ces théorèmes doivent être vrais, se dit-il alors, car s'ils ne l'étaient pas, personne n'aurait assez d'imagination pour les inventer. » Les résultats de Ramanujan font le tour des mathématiciens de Cambridge, qui sont unanimes : derrière ces formules doit se trouver un véritable génie.
Conquis, Hardy renvoie une lettre à Ramanujan, dans laquelle il lui exprime tout son intérêt et son admiration et lui annonce qu'il souhaite vivement le rencontrer pour discuter de ses résultats.

Le jeune homme de 27 ans se lance donc dans l'aventure. Il quitte les côtes indiennes par bateau pour rejoindre Londres, puis Cambridge, où il arrive en avril 1914. Rapidement, il se met au travail, laissant Hardy accéder librement à ses carnets pour les étudier. À leur lecture, Hardy découvre l'étonnant potentiel de Ramanujan. Débute alors une étonnante collaboration entre les deux hommes, que tout oppose. Les deux mathématiciens ont en effet des personnalités, des cultures, des croyances, mais également des styles de travail totalement opposés. Alors que Ramanujan fonctionne à l'instinct et à l'intuition, présentant ses résultats de manière non structurée, Hardy est un fervent partisan des démonstrations et d'une approche mathématique très rigoureuse.

Malgré cela, la collaboration entre les deux hommes s'avère très fructueuse et produit un grand nombre de résultats, largement publiés dans les journaux scientifiques. Car Ramanujan s'avère être un chercheur très prolifique.
Une santé fragile
Mais la santé fragile de Ramanujan le rattrape et le maintien de son régime alimentaire strictement végétarienvégétarien que lui impose sa religion brahmane lui cause de plus en plus de soucis. Son premier hiverhiver en Angleterre s'avère particulièrement difficile. Il se retrouve ainsi en carencecarence sévère de vitaminesvitamines. Diagnostiqué tuberculeux, il est forcé de prendre du repos et de ralentir son rythme de travail.
Ses travaux sont cependant de plus en plus reconnus et en mars 1916, sur la base de ses résultats sur les nombres hautement composés, l'université de Cambridge décide de lui délivrer le grade de docteur en mathématiques, bien qu'il n'ait pas suivi le cursus traditionnel.

Sa santé continue néanmoins de se dégrader et, en 1917, il tombe très sérieusement malade. Durant les mois qui suivent, il passe ainsi d'hôpital en hôpital. Si ses collègues sont particulièrement inquiets pour lui, Ramanujan se veut plutôt fataliste et continue sa recherche depuis sa chambre de convalescence.
La maladie ne l'empêche pas de continuer à échafauder de nouvelles théories et en février 1918 il est admis comme membre de la Cambridge Philosophical Society en reconnaissance de ses travaux scientifiques. La même année, il est élu à la Royal Society de Londres sur la proposition d'une impressionnante liste de mathématiciens. Le Trinity College de Cambridge lui alloue également un poste pour une durée de six ans. Les honneurs pleuvent sur le jeune indien de 31 ans qui peine cependant à recouvrer sa santé.
La fin de la guerre autorise cependant à nouveau les voyages internationaux et Ramanujan décide, malgré le poste offert, de retourner en Inde. Il embarque en février 1919. À son arrivée, il intègre directement l'université de Madras avec une réputation scientifique telle qu'aucun Indien avant lui n'a jamais connu.
Des milliers de formules léguées à la postérité
Mais son corps semble à bout de souffle. Malgré de nombreux traitements, il finira par mourir l'année suivante, en 1920, à l'âge de 32 ans seulement. L'analyse de son dossier médical dans les années 1990 révèlera qu'il souffrait très certainement d'une amœbose hépatique, maladie liée à la présence d'un parasite intestinalparasite intestinal et qui pourrait être une complication de précédents épisodes de dysenteriedysenterie.
De l'avis de Hardy, si le don de Ramanujan avait été reconnu plus tôt, il aurait pu devenir l'un des plus grands mathématiciens de tous les temps. Dans les séries hypergéométriques et les fractions continues, « il était incontestablement l'un des grands maîtres ». Mais sa contribution principale réside en tous ces petits carnets de notes dans lesquels il consignait les formules qui semblaient jaillir de son esprit. Les carnets retrouvés après sa mort renfermaient en effet plusieurs milliers de formules. Si certaines étaient déjà connues, d'autres fausses, la grande majorité étaient exactes et parfois associées à des théories profondes et complexes encore inconnues à l'époque. L'analyse de ces formules prendra au total près d’un siècle et occupera plusieurs générations de mathématiciens. Srinivasa Ramanujan apparaît donc comme un mathématicien tout à fait unique, se basant sur un fonctionnement cérébral différent, qui continue, encore aujourd'hui, à fasciner les scientifiques.









