au sommaire

Terence Tao
Surdoué, docteur à l'âge de 21 ans, l'australien Terence Tao est le plus jeune des mathématiciensmathématiciens récompensés à Madrid en août 2006 par la plus illustre des distinctions dans cette discipline : la médaille Fields. Il est l'auteur de travaux originaux aussi nombreux que variés dans les thèmes : de l'analyse harmonique à l'arithmétique, en passant par la combinatoire ou la théorie des représentations, TT. Tao refuse de segmenter sa discipline. Cet article propose de revenir sur deux de ses résultats les plus notoires, l'un concernant les nombres premiers en progression arithmétique, l'autre les conjectures de Kakeya.Nombres premiers en progression arithmétique Depuis l'antiquité grecque, il est bien connu qu'il existe une infinité de nombres premiers (EuclideEuclide, livre IX des Éléments)). En 1785, pour démontrer une importante prédiction de la théorie des nombres (la loi de réciprocité quadratique), Legendre a besoin de plus et suppose qu'une suite arithmétique a+nb contient toujours une infinité de nombres premiers à condition que a et b soient premiers entre eux (i.e. n'ont pas de diviseurs communs excepté 1). Il faudra néanmoins attendre Dirichlet (1837) pour justifier cette hypothèse car la tâche est au moins aussi difficile que de prouver la loi de réciprocité quadratique elle-même...
Cet article fait partie d'une série spéciale médaille Fields :
- Wendelin Werner, le seigneur des zigzags (08/09/06)
- Andreï Okounkov, des probabilités à la théorie des cordes (19/09/06)
Nombres premiers en progression arithmétique
Depuis l'antiquité grecque, il est bien connu qu'il existe une infinité de nombres premiers (Euclide, livre IX des Éléments). En 1785, pour démontrer une importante prédiction de la théorie des nombres (la loi de réciprocité quadratique), Legendre a besoin de plus et suppose qu'une suite arithmétique a+nb contient toujours une infinité de nombres premiers à condition que a et b soient premiers entre eux (i.e. n'ont pas de diviseurs communs excepté 1). Il faudra néanmoins attendre Dirichlet (1837) pour justifier cette hypothèse car la tâche est au moins aussi difficile que de prouver la loi de réciprocité quadratique elle-même...

La suite arithmétique 3+4n : elle contient une infinité de nombres premiers (en rouge).
Crédits : S. Tummarello.
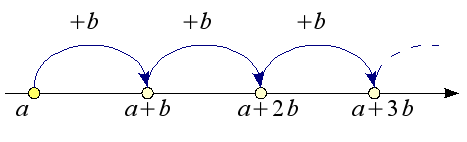
Une suite arithmétique est une suite logique ou chaque terme est calculé à partir du précédent en ajoutant le même nombre.
Crédits : S. Tummarello.
Les travaux de T. Tao et B. Green portent sur une question similaire : s'il existe des séquences de nombres premiers régulièrement espacés telle que 3, 7 et 11, ou mieux 359, 389, 419, 449, 479 et 509, peut-on en trouver de plus longues ? Le record à ce jour est détenu par M. Frind, P. Jobling et P. Underwood qui ont présenté en 2004 la séquence 56211383760397 + 44546738095860 x n pour n entier compris entre 0 et 22, soit 23 nombres premiers. La compétition risque toutefois de durer car T. Tao et B. Green ont montré qu'il existe des progressions arithmétiques en nombre premiers aussi longues que l'on veut ! Une courte histoire du théorème de Green-Tao Comment les nombres premiers sont ils répartis ? La stratégie moderne pour tenter de pénétrer ce mystère remonte à Riemann et à son article fondateur de 1859 : le comportement de la fonction Π(N), qui compte les nombres premiers inférieurs à un nombre N, est codé dans un objet mathématique appelé fonction ζ (zêta) de Riemann. Cette approche s'est avéré très fructueuse car elle a permis à Hadamard et De La Vallée Poussin de venir à bout du « théorème des nombres premiers » en 1896 : la "densité de nombres premiers" Π(N)/N est asymptotiquement équivalente à 1/log N.
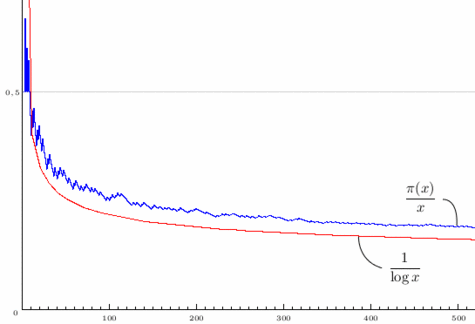
Le théorème des nombres premiers : la densité des nombres premiers (en bleu) se comporte aymptotiquement comme l'inverse du logarithme (en rouge).
Crédits : S. Tummarello.
Néanmoins, la distribution précise des nombres premiers demeure une question ouverte d'une extraordinaire difficulté, et il n'est pas surprenant que l'approche de T. Tao ne soit pas frontale. Plutôt que de chercher des informations supplémentaires sur la sibylline fonction ζ, T. Tao a attaqué le problème "par la face sud", en étudiant les propriétés des ensembles de nombres ne contenant aucune progression arithmétique, pour lesquels quelques résultats étaient déjà connus. Erdös, célèbre pour ses défis inextricables, avait en effet promis en 1936 la somme de 10.000$ à qui résoudrait l'énigme suivante : étant donnés deux entiers N et k, quel est le plus grand nombre (noté ρk(N)) d'entiers inférieurs1 à N que l'on peut collecter sans que parmi eux apparaisse une progression arithmétique de longueur k2 Pour illustrer la question, calculons ρ3(6) : on peut vérifier que parmi cinq entiers choisis plus petits que 6, trois sont nécessairement consécutifs, mais que l'ensemble 1, 3, 4, 6 ne contient pas de progression arithmétique de longueur 3. Ainsi ρ3(6)=4. Une idée naturelle serait donc d'établir que pour tout k, Π(N) > ρk(N) à partir d'un certain rang : le théorème de Green-Tao s'en déduirait aussitôt. La discussion n'est hélas pas si simple : si K. Roth (1953) et surtout E. Szemerédi (1969, 1975) ont accompli des percées décisives en prouvant que le rapport ρk(N)/N tend vers zéro quand N augmente (k=3 par Roth, puis k=4 et k quelconque par Szemerédi), personne n'a pu exhiber une majoration explicite, i.e. une fonction ωk(N) de limite zéro en l'infini telle que ρk(N)/N k(N) ! B. Green souligne cette difficulté : « le théorème de Szemerédi fait partie de ces nombreux résultats en combinatoire pour lesquels les bornes, s'il est seulement possible de les mettre en évidence, sont d'une lenteur presque inconcevable. »3. En d'autres termes, la décroissance de ρk(N)/N est "infiniment" dérisoire comparée à celle du rapport Π(N)/N ~ 1/log N ou même des inverses des itérés du logarithme ! Il ne semble donc guère raisonnable d'espérer une solution simple par cette voie.
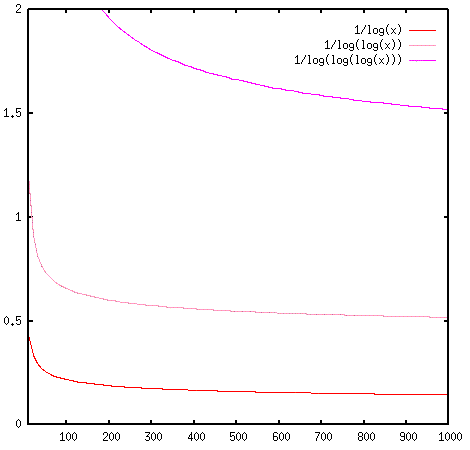
Ordres de grandeur : les inverses des premiers itérés du logarithme (1/log log et 1/log log log) décroissent beaucoup plus lentement vers zéro que 1/log N. Graphique obtenu à l'aide du logiciel gnuplot.
Cependant, deux nouvelles preuves du théorème de Szemerédi sont publiées en 1977 et 1998 : la première par H. Furstenberg relève de la « théorie ergodique », et la seconde, de T. Gowers, utilise « l'analyse de Fourier non-linéaire ». En s'inspirant des nouvelles idées contenues dans ces démonstrations, T. Tao et B. Green ont ainsi pu construire des outils ad hoc (comme les « mesures pseudo-aléatoires ») qui, ajoutés à des lemmes techniques récents dus à D. Goldston et C.Y. Yildirim (2003), leur ont permis de réaliser leur coup de maître en 2004. Le problème de Kakeya À vos crayons ! Comment retourner une aiguille (de longueur 1) dans le plan de sorte qu'elle balaie une aire la plus petite possible ? Si vous pensez à faire tourner l'aiguille sur elle même, l'aire balayée est celle d'un disque de diamètre 1, soit Π/4. Mais pour le mathématicien japonais S. Kakeya, l'aire minimale est celle délimitée par une « deltoïde », soit Π/8 (1917).
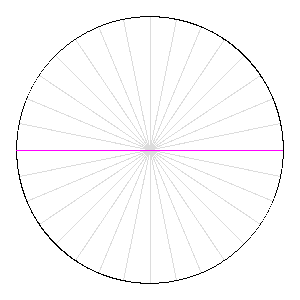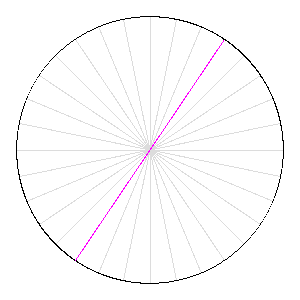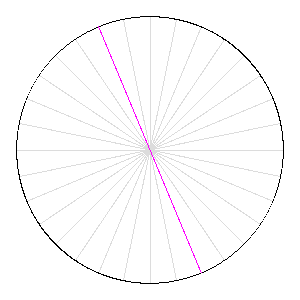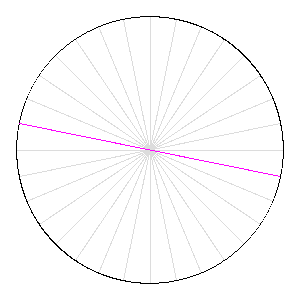
Rotation d'une aiguille sur elle-même : l'aire balayée vaut celle du disque.
Crédits : S. Tummarello.
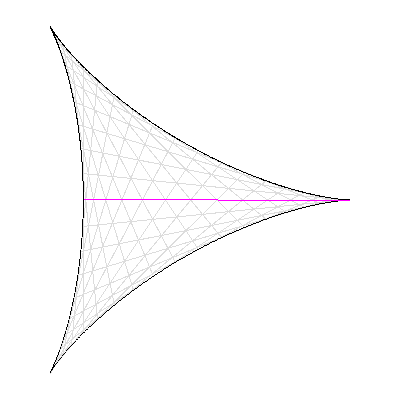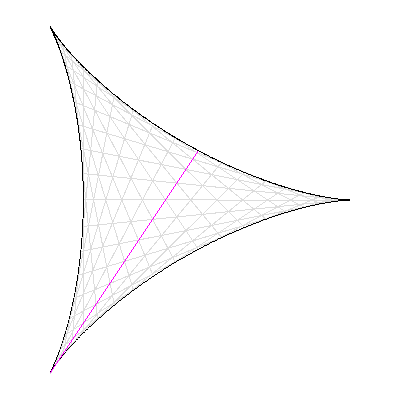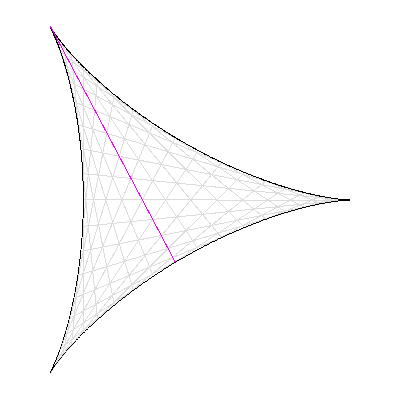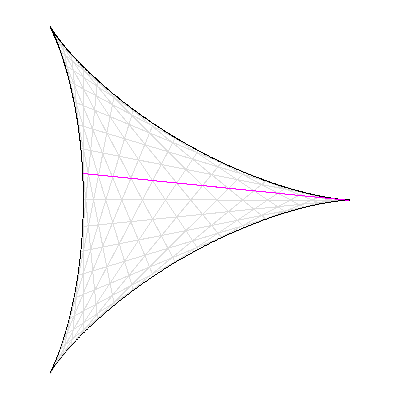
Conjecture de Kakeya : la surface minimale pour retourner une aiguille est délimitée par une deltoïde.
Crédits : S. Tummarello.
Pourtant, Besicovitch stupéfait la communauté mathématique en 1928 en montrant que la conjecture de Kakeya s'avère fausse au point que l'on peut retourner une aiguille dans un domaine du plan d'aire aussi petite que l'on veut ! Sa méthode repose en premier lieu sur le fait qu'il est possible de translater l'aiguille en balayant une aire aussi minime que souhaité : il suffit de la faire glisser « très loin », d'effectuer une légère rotation, puis revenir pour finalement la disposer parallèlement à sa position initiale. Cette remarque permet de ramener le problème de Kakeya à la recherche de domaines du plan qui contiennent un segment unité dans toutes les directions.

Simplification de Besicovitch : la translation d'une aiguille peut s'effectuer en balayant une aire arbitrairement petite.
Crédits : S. Tummarello.
Besicovitch a ainsi donné son nom aux domaines d'aire nulle qui possèdent cette propriété de contenir un segment unité dans toutes les directions. Il existe de nombreuses façons de construire de tels ensemble, celle que nous présentons est due à PerronPerron (1928). Partons d'un triangle rectangle dont deux côtés sont de longueur 1 : on peut y disposer l'aiguille de Kakeya de sorte qu'elle forme avec la verticale un angle quelconque compris entre 0° et 45°. Découpons le triangle selon une bissectrice et recouvrons partiellement un des deux nouveaux triangles par l'autre : on obtient alors un polygone qui peut toujours contenir une aiguille dans toutes les directions comprises entre 0° et 45°, mais dont l'aire est moindre que celle du triangle de départ (voir figure). En répétant indéfiniment le procédé, on construit un « arbrearbre de Perron », qui est d'aire nulle mais qui contient un segment unité selon toutes les orientations entre 0° et 45°. Il suffit dès lors de copier par symétries l'arbre de Perron pour obtenir un exemple d'ensemble de Besicovitch.

Construction de l'arbre de Perron.
Crédits : S. Tummarello.
Dimensions des ensembles de Besicovitch Les mathématiciens se sont vite affranchi du plan pour généraliser la conjecture de Kakeya aux espaces à n dimensions : à nouveau le volume minimal pour orienter une aiguille dans toutes les directions est nul. Si le volume ne fournit par conséquent aucune information pertinente sur la manière dont les ensembles de Besicovitch remplissent l'espace, la dimension fractale joue précisément ce rôle : elle généralise à des quantités non-entières la notion usuelle de dimension (le nombre de coordonnées nécessaires pour situer un point). Le célèbre tapis de Sierpinski est par exemple de dimension fractale log(3)/log(2) ~ 1,58. Redécouvrez à ce sujet l'excellent dossier de Jean-Pierre LouvetJean-Pierre Louvet : Les fractales.

Un exemple célèbre de fractale : le tapis de Sierpinski.
Crédits : S. Tummarello.
Sans entrer dans les définitions techniques, il existe plusieurs façons de calculer la dimension fractale d'un ensemble géométrique. Tandis que la dimension fractale fait habituellement référence à la dimension de Hausdorff, c'est souvent la dimension de Minkowski qui est présentée (car relativement plus simple à énoncer). Ceci ne prête pas à confusion pour les figures fractales car elles ont des propriétés de self-similarité ; mais les deux notions ne coïncident pas toujours et la distinction s'impose dans le cas des ensembles de Besicovitch pour lesquels on ne connaît ni la dimension de Hausdorff, ni celle de Minkowski. S'il est conjecturé que toutes deux soient maximales (donc de valeur n, la dimension de l'espace ambiant), seul le cas n=2 a été réglé, en 1971 par Davies. T. Tao s'est affirmé comme l'expert de ces conjectures en apportant des contributions essentielles à leur compréhension : en particulier, il a démontré en 1999 que les ensembles de Besicovitch sont de dimension de Minkowski au moins (4n+3)/7, et de dimension de Hausdorff4 au moins (6n+5)/11. Ces bornes sont les meilleures connues à ce jour. Un problème d'une portée insoupçonnée Le casse-tête de Kakeya peut sembler gratuit au premier abord, mais il se trouve en fait relié à des problèmes profonds de convergence en analyse harmonique, une des sphères de prédilection de T. Tao. Connue aussi sous le nom de théorie de Fourier, ce domaine traite à l'origine (1822) de la décomposition de signaux périodiques en ondes sinusoïdales simples. Réciproquement, un théorème fondamental (la formule d'inversion de Fourier) permet de reconstruire un signal à partir de ses harmoniques. Depuis, la théorie s'est considérablement développée au point de constituer un instrument incontournable non seulement pour les mathématiques, mais aussi pour de multiples autres disciplines.
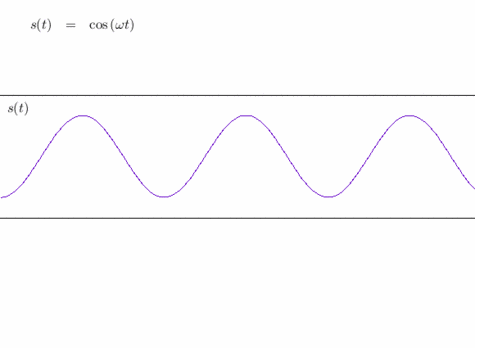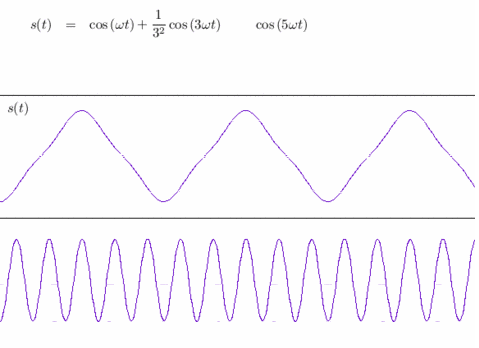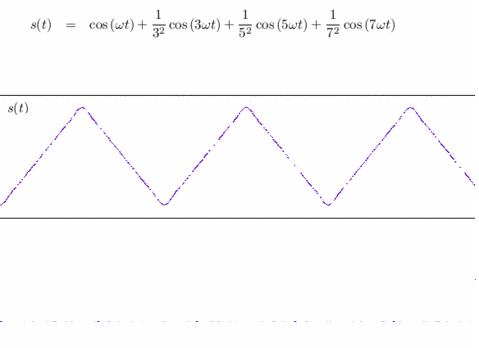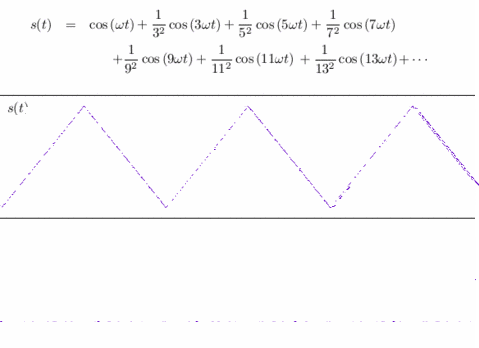
Reconstitution d'un signal triangulaire à partir de sa décomposition en harmoniques (sinusoïdes).
Crédits : S. Tummarello.
À la surprise générale, C. Fefferman a montré en 1971 que la situation est étrangement très différente pour des "signaux" dont la dimension vaut 2 ou plus : de graves problèmes de convergence apparaissent, précisément du fait de l'existence des ensembles de Besicovitch5. De même, si un ensemble de Besicovitch avait une dimension de Hausdorff strictement inférieure à n, alors la conjecture de Bochner-Riesz, qui tente grosso modo de rétablir la convergence sous une autre forme, serait fausse. L'exactitude ou non des conjectures de Kakeya a ainsi des conséquences très concrètes en analyse harmonique, une branche des mathématiques qui n'a cessé d'apporter des moissons d'applications technologiques (dont la compression du son et de l'image par exemple). Nids d'abeilles Pour conclure cet article, citons la résolutionrésolution presque magique par T. Tao et A. Knutson d'une conjecture formulée par Horn en 1962 et répondant à une question de H. Weyl datant de 1912 (connaissant les valeurs propres de deux matrices hermitiennes A et B, que peut-on dire de celles de la somme A+B ?). La grande astuce de la démonstration réside dans l'étude de ce que T. Tao a baptisé des « nids d'abeilles ».
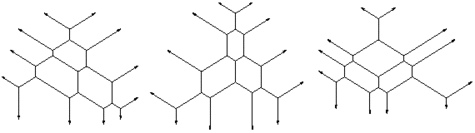
Nids d'abeilles de Terence Tao.
Du reste, et de l'aveu du lauréat, le lien entre la conjecture de Horn et les nids d'abeilles demeure un mystére qui, une fois compris, aura selon lui « un impact significatif à la fois en théorie des représentations et en géométrie symplectique »6. À bon entendeur... 1 Sans précision le terme « inférieur » (ou « plus petit ») est à prendre au sens large, à savoir : « inférieur ou égal ». 2 Plus précisément, et comme il n'est guère probable d'obtenir une formule explicite, Erdös demandait "juste" une estimation asymptotique dans le cas où k=3... Estimation qui demeure cependant inconnue à ce jour ! 3 « Szemerédi's theorem is one of many in this branch of combinatorics for which the bounds, ifif they are ever worked out, are almost unimaginably weak. ». B. Green, Long arithmetic progressions of primes, 2005, p.4. 4 La dimension de Hausdorff est toujours plus petite ou égale à la dimension de Minkowski. 5 Si
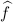
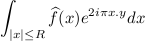
- <//li><//li>






















