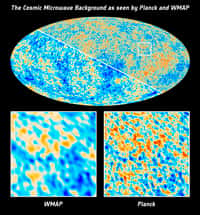
au sommaire

Jean-Pierre Luminet. Crédit : OBSPM
Déjà en 2003, les résultats fournis par WMap sur le spectre de puissance des fluctuations dans le rayonnement fossile pouvaient être interprétés comme une indication d'une taille finie de notre Univers. Mieux, on pouvait aussi y trouver des indices en faveur d'une topologie particulière de l'espace, une possibilité étudiée depuis des années par Jean-Pierre Luminet et certains de ses collaborateurs, comme les astrophysiciensastrophysiciens Marc Lachièze-Rey et Roland Lehoucq.
Pour comprendre de quoi il s'agit, nous prendrons l'exemple d'un Univers fictif (voir la figure 1), en forme de cylindre sur lequel se balade un petit insecteinsecte. On peut construire un tel Univers en partant d'un carré et en identifiant deux de ses bords. L'opération revient à coller ceux-ci et l'on voit que tout se passe comme si l'insecte se déplaçant sur le carré et voulant sortir de celui-ci rentrait automatiquement dans ce même carré mais par le bord opposé.
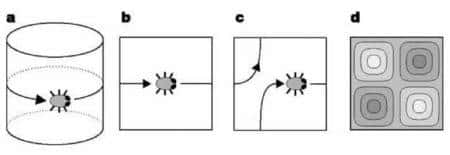
Figure 1. La longueur d'onde des fluctuations de densité est limitée par la taille d'un univers se refermant sur lui-même. Schéma a : une créature vivant à la surface d'un cylindre se déplace et revient à son point de départ après avoir fait un tour complet. Schéma b : un cylindre découpé se transforme en un carré et le trajet de la créature sort par le côté droit pour entrer par le côté gauche. Schéma c : un tore plat est aussi construit à partir d'un carré dont on identifie les côtés opposés ; un tel espace est dit multi-connexe. Schéma d : des ondes se propageant dans un univers torique ne peuvent pas avoir une longueur d'onde supérieure au côté du carré. Pour construire un espace multi-connexe à trois dimensions, on identifie deux à deux les faces d'un polyèdre, un cube par exemple. Dans une telle configuration, la forme des ondes autorisées à se propager dépend de la géométrie de l'espace et de la façon dont les faces sont associées. Crédit : OBPSM
Une des caractéristiques d'un tel Univers à deux dimensions où vivraient des être bidimensionnels est que des rayons lumineux émis par des objets pourraient faire le tour de cet Univers et donner lieu à des images fantômes, laissant croire à un observateur qu'il est dans un monde infini peuplé d'un très grand nombres d'objets possédant des formes identiques.
Si l'on identifie les deux autres bords du carré, cela revient à coller les sommets du cylindre et on obtient un nouvel Univers en forme de pneupneu, possédant la même géométrie plate que le précédent et les mêmes images fantômes indiquant un Univers infini.
Notre propre Univers pourrait bien ressembler à un Univers en forme de tore, avec une géométrie plate (voir la figure 2).

Figure 2
Notre Univers apparaît en effet comme remarquablement homogène et isotrope, avec des régions de l'espace occupées par un rayonnement fossile dont la température est identique à un degré de précision époustouflant. Sa géométrie spatiale est très proche de la géométrie euclidienne. On comprend mal comment un tel Univers a pu émerger du Big BangBig Bang, alors que les régions qui le composaient n'avaient pas eu le temps d'échanger de la chaleur à la vitesse de la lumièrevitesse de la lumière pour atteindre ce remarquable degré d'homogénéité dont témoigne le rayonnement fossile.
Une solution est bien sûr la théorie de l'inflation, très favorisée par les données de WMap, mais une autre est de dire que notre Univers est en réalité bien plus petit que l'on ne le croit et qu'en conséquence, les régions que nous observons avaient eu le temps de communiquer entre elles au moment du Big Bang (voir toutefois la mise au point à ce sujet de Jean-Pierre Luminet). Sa grande taille ne serait qu'une illusion d'optique similaire à celle que nous avons décrite avec les exemples précédents.
L'apparente infinité de notre Univers est-elle une illusion d'optique ?
Lorsque l'on veut étudier les formes possibles de l'espace, on utilise une théorie mathématique appelée la topologie. Ainsi une sphère et un ballonballon de rugby sont topologiquement équivalents, car l'on peut déformer l'une en l'autre sans faire de trou. Ce n'est pas le cas d'un tore et d'une sphère.
Jean-Pierre LuminetJean-Pierre Luminet et ses collègues ont donc cherché des alternatives à l'inflation pour expliquer les caractéristiques étonnantes de l'Univers en utilisant des Univers topologiquement différents mais de taille finie plus petite que celle déduite des observations avec des modèles classiques d'Univers à la Friedmann-Lemaître (Robertson-Walker).
Le meilleur candidat pour coller aux observations de WMap semble être le dodécaèdre de Poincaré. Pour comprendre de quoi il retourne considérons une sphère avec un pavage en forme de ballon de football :

Figure 3. Crédit : OBSPM
Cela revient à considérer un dodécaèdre :
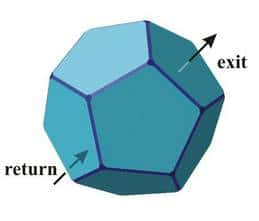
Figure 4. Crédit : OBSPM
On joue ici le même jeu qu'avec le carré initial en deux dimensions mais on a affaire à un polyèdre en trois dimensions dont on va identifier les côtés opposés. On obtient ainsi une sorte de multi-tore mais qui n'en est pas vraiment un. L'espace dodécaédrique de Poincaré (PDS), en gros, c'est cela...
Or, de même qu'une corde peut osciller selon différents modes stationnaires dépendant de la longueur de la corde, un instrument de musique, comme un tambour ou un violon, ne pourra produire que des sons caractéristiques de sa taille et de sa forme. Ainsi, lors de la « création » de l'Univers observable, le fluide de particule occupant l'Univers était animé de modes de vibrationsvibrations dépendant de la forme géométrique de notre Univers, de sa composition en particules et aussi de sa topologie.
Dans le cas d'un Univers fini possédant une topologie obtenue par identification des faces d'un polyèdre donné, on peut calculer, en théorie du moins, les modes possibles d'oscillations et faire des prédictions sur la forme précise du spectre du rayonnement fossile. Remarquablement, certains des Univers finis avec une topologie dite multiplement connexeconnexe conduisent donc à des hypothèses testables et, si nous vivons dans un de ces Univers, nous pouvons le savoir !
La figure 5 montre quelques exemples d'Univers avec topologie multiplement connexe -- Luminet parle d'Univers chiffonnés --, avec la structure du rayonnement fossile à laquelle ils conduisent.
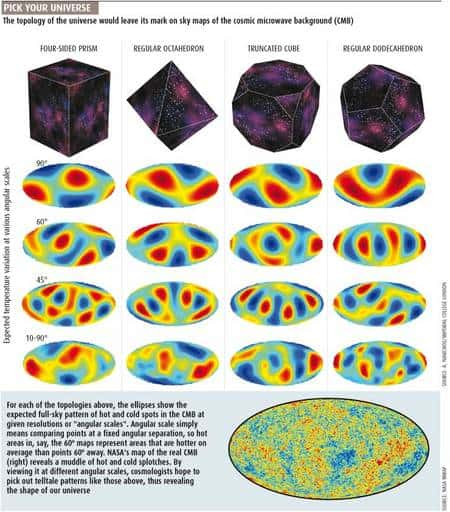
Figure 5. Crédit : New Scientist
Depuis, l'année 2003 et la publication dans Nature d'un article dans lequel Jean-Pierre Luminet et ses collègues proposaient le Poincare Dodecahedral Space(PDS), les chercheurs ont progressé dans le calcul du spectre de puissance que devait avoir le rayonnement fossile.
Ainsi, 1,7 milliard de modes vibrationnels sont maintenant connus et pris en compte dans la comparaison avec les données de WMap. Il en résulte que le modèle PDS fait aussi bien que le modèle Lambda CDM (constante cosmologiqueconstante cosmologique-matière noirematière noire) avec un Univers plat, infini et à la topologie simplement connexe, alors que dans le premier on est en présence d'un Univers clos, donc fini, et à la topologie multiplement connexe. Si l'on considère la densité totale de l'Univers ramené à celle de la densité critiquedensité critique, on trouve alors pour ce rapport 1,018 .
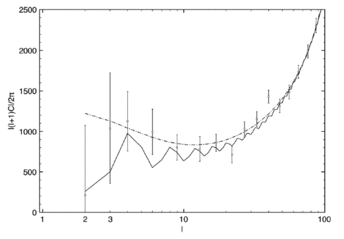
Figure 6. Cliquez sur l'image pour l'agrandir. Spectres de puissance comparés pour les données expérimentales de WMap (barres d'erreur verticales), pour le modèle théorique LambdaCDM (courbe en pointillés) et pour le modèle PDS (courbe pleine). Crédit : OBSPM
Comment départager les deux théories ?
Peut-être en suivant la voie explorée depuis des années par Boudewijn Roukema, à la tête d'une équipe polonaise qui, elle aussi, annonce avoir obtenu des résultats encourageants en faveur du modèle PDS.
Examiné de près, le processus d'identification des faces du dodécaèdre conduit à des corrélations entre les images que l'on peut obtenir de la surface de dernière diffusiondiffusion (voir la figure 7), correspondant pour chaque observateur dans l'Univers au moment où le rayonnement fossile a été émis. On montre que ces corrélations reviennent à considérer des intersections des images de ses surfaces sphériques et qu'elles conduisent à toute une série de cercles anti-podaux le long desquels les corrélations sont observables.
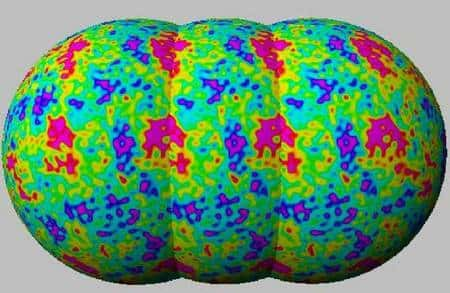
Figure 7. Une topologie multiconnexe se traduit par le fait que tout objet de l'espace peut se présenter en de multiples exemplaires au sein de l'univers observable. Pour un objet étendu comme la région d'émission du rayonnement fossile, appelée surface de dernière diffusion, celle-ci peut s'auto-intersecter le long de paires de cercles. En ce cas, cela revient à dire qu'un observateur (situé nécessairement au centre de cette surface de dernière diffusion) verra la même région de l'univers dans différentes directions. En conséquence, les fluctuations de température seront identiques le long des paires de cercles d'auto-intersection de la surface de dernière diffusion, comme le montre la figure.
Cette carte du rayonnement fossile a été calculée pour un espace plat multi-connexe, précisément un hypertore dont la taille est 3,17 fois inférieure au diamètre de l'horizon cosmologique. Crédit : OBSPM
Tout le problème, et il est de taille, est d'extraire de façon convaincante ces zones des mesures effectuées par WMap et de montrer qu'il existe bien des corrélations qui ne peuvent statistiquement se produire que de façon très improbable dans un Univers LambdaCDM. L'équipe de Boudewijn Roukema avait déjà obtenu il y a quelques années des résultats dans ce sens, et elle confirme à nouveau la possible présence de ces cercles.
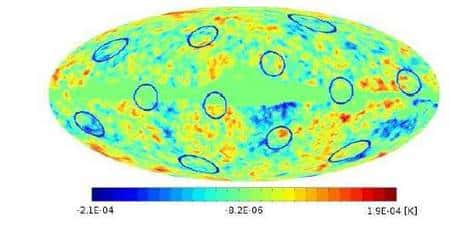
Figure 8. Position des 12 cercles corrélés trouvés récemment dans les données WMap par une équipe franco-polonaise, en parfait accord avec le modèle PDS. Les centres des cercles correspondent aux centres des faces du dodécaèdre fondamental, déterminés par leurs coordonnées galactiques. La probabilité pour que le modèle LambdaCDM plat et infini reproduise par hasard une telle configuration n'est que 7 %. Crédit : OBSPM
Malheureusement, même si ces résultats sont plus précis, ils ne sont toujours pas probants. En revanche, on peut penser que les choses vont s'améliorer avec le lancement prochain du satellite PlanckPlanck par l'Esa.
Quelques considérations de cosmologie quantique
Pour finir, si l'on se place du point de vue de la cosmologie quantique, on sait depuis longtemps que des Univers clos à courbure positive sont favorisés par l'approche reposant sur l'intégrale de chemin de Feynman. Comme l'ont montré Stephen HawkingStephen Hawking et James Hartle avec leur modèle sans bord et utilisant le temps imaginaire, il est plus naturel, mais pas démontré, de considérer des Univers clos que des Univers infinis.

James Hartle. Crédit : University of California, Santa Barbara
En adoptant l'approche de la théorie des cordesthéorie des cordes, qui introduit des objets géométriques topologiquement compliqués comme les espaces de Calabi-Yau et les orbifolds, il est également plus naturel de considérer l'espace-tempsespace-temps macroscopique comme une partie d'un espace-temps multidimensionnel et topologiquement multiconnexe qui serait entré en expansion aux dépens d'autres dimensions qui, elles, seraient restées microscopiques.
Inutile de dire que dans le cadre des discussions actuelles, souvent chaudes, sur le principe anthropique, le Landscape, les cerveaux de Boltzmann, la possibilité d'un Univers fini ne manquera pas d'être appréciée...