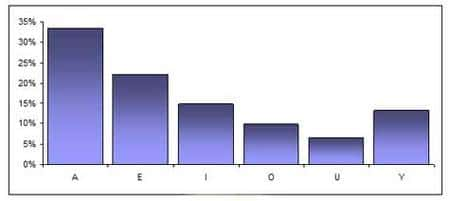
au sommaire

Hasard, logique et mondes parallèles
La théorie de la complexité pourrait clore le débat sur le hasard... sauf qu'elle ne s'applique qu'aux suites infinies, et laisse en suspens la question de définir un évènement aléatoire qui ne se produit qu'une fois. Si je dis que j'ai rencontré Paul « par hasard », je veux probablement dire (c'est une des définitions intuitives courantes) que j'aurais pu ne pas le rencontrer.
Un évènement aléatoire serait donc, selon cette conception un peu vaguevague, un évènement fortuit, c'est-à-dire possible, mais non nécessaire. Paradoxalement, c'est du côté de la logique mathématique que l'on trouvera le moyen d'une définition formelle de la contingence, et donc d'un évènement aléatoire non répété.

« J’aurais pu ne pas être là » peut être pris, en première approximation, comme synonyme de « je suis là par hasard ».
La logique classique n'est pourtant d'aucun secours. En logique classique, tout ce qui est vrai est possible et nécessaire, tout ce qui est faux est impossible. Il ne reste guère de place pour le contingent. Mais la logique mathématique ne s'arrête pas à la logique classique : des penseurs ont en effet fabriqué des modèles plus souples que l'on appelle judicieusement des logiques « non-classiques ». Parmi ces théories, la logique des mondes possibles, inventée par Saül Kripke il y a quelques décennies, nous intéresse particulièrement.
Mondes parallèles
Une manière parmi d'autres de concevoir l'idée générale de la logique des mondes possibles est d'imaginer des mondes parallèles, qui sont les mondes possibles (pour une brève introduction plus mathématique, voir mon livre Vous avez dit hasard ? Entre mathématiques et psychologie, Belin, 2009 dernière page de ce dossier).
Par exemple, dans tel monde possible l'Allemagne a gagné la seconde guerre mondiale. Dans tel autre, Barack Obama a perdu les élections. À chaque instant, on peut imaginer une infinité de mondes possibles. Dans le film The One, avec Jet Li, un individu passe d'un monde parallèle à l'autre grâce à une machine : c'est là une illustration des mondes possibles de Kripke.

« Les mondes parallèles », tableau de Mauricio Escobar (détail).
Hasard et passé
Lorsque le temps passe, nous voguons d'un monde possible à l'autre. Ce passage suit certaines règles : depuis chaque monde, certains sont accessibles et d'autres non. Par exemple, à partir d'un monde où Barack Obama n'est jamais né, nous ne pouvons pas atteindre notre monde actuel. Les écologistes les plus pessimistes pensent par exemple qu'aucun monde possible viable en 2300 n'est accessible depuis celui où nous évoluons aujourd'hui.
Compte tenu de ces contraintes, certains évènements sont accessibles, d'autres non. Si l'on suppose qu'à partir de notre monde actuel, il est possible d'atteindre un monde où InternetInternet disparaît et un autre où Internet perdure en 2030, alors nous pourrons dire que l'existence éventuelle d'Internet en 2030 serait fortuite. Autrement dit encore, il est possible qu'Internet existe encore, mais pas nécessaire. Du coup, nous pouvons qualifier l'existence d'Internet en 2030 d'événement aléatoire.
Plaçons-nous maintenant en 2030, et supposons qu'Internet existe toujours. À ce moment, l'existence d'Internet en 2030 sera devenue nécessaire, si bien qu'un événement aléatoire à un moment cesse d'être aléatoire lorsqu'il s'est produit. C'est une caractéristique du hasard que les philosophes, comme le rappelle Marcel Conche, ont depuis longtemps noté : le hasard s'applique toujours à l'avenir, jamais au passé.
La logique des mondes possibles fournit ainsi une définition formelle du hasard, qui malheureusement s'applique mal à la réalité, puisqu'on ne connaît pas les mondes possibles... néanmoins, elle prouve que nous pouvons non seulement formaliser l'idée de suite aléatoire, avec la complexité, mais aussi celle d'évènement aléatoire, en partant d'une conception naturelle du hasard.