au sommaire
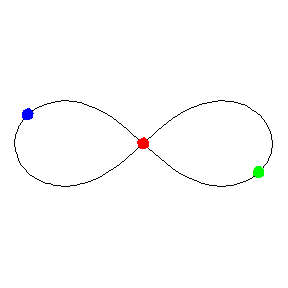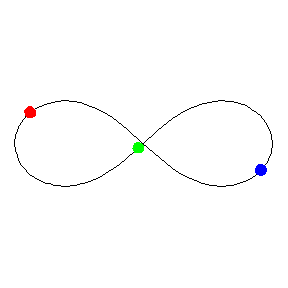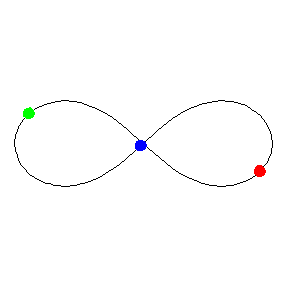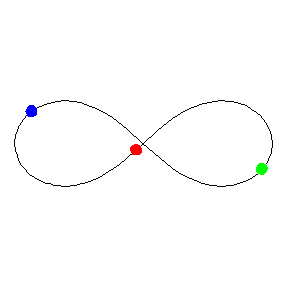
Crédit : Michael Nauenberg
Cette étonnante orbite fermée fait partie des orbites similaires dites chorégraphiques et, bien qu'elle ait été découverte en 1993, la démonstration rigoureuse de son existence et surtout de sa stabilité n'a été faite qu'en 2000 par Chenciner et Montgomery. Pour tous ceux qui penseraient qu'il n'y a plus rien à découvrir dans des domaines aussi anciens que ceux de la mécanique céleste, que ce soit en physique Newtonienne ou en relativité générale, les résultats obtenus par Tatsunori Imai, Takamasa Chiba et Hideki Asada de l'Université de Hirosaki viennent de prouver le contraire.
Les corrections aux équations de mouvements de N corps dans le cadre de la mécanique céleste relativiste font partie de ce qu'on appelle l'approximation post-Newtonienne en relativité générale. Elles sont en grande partie l'œuvre du travail conjoint d'EinsteinEinstein et ses collaborateurs Léopold Infeld et Banesh Hoffman
Pour donner une idée de la complexité des équations obtenues, il suffit de jeter un coup d'œilœil sur la fonction dite de Lagrange, L, donnant les corrections en première approximation à celle de la mécanique Newtoniennemécanique Newtonienne. Les équations de mouvements de A=1, 2, 3... n corps y sont données par les deux premiers termes de la fonction de Lagrange relativiste corrigée ci-dessous.
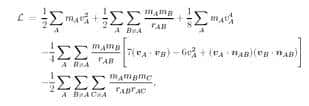
On y reconnaît l'énergie cinétiqueénergie cinétique en premier et l'énergie potentielleénergie potentielle gravitationnelle d'interaction entre les corps en physique classique en second. Comme à son habitude on a utilisé un système d'unités dans lequel G et c valent 1. On mesure donc à quel point l'existence de cette orbite chorégraphique n'était pas du tout garantie dans le cadre de la RG. L'ordinateurordinateur a pourtant montré que, moyennant de bonnes conditions initiales, l'orbite en forme de 8 se maintenait pendant au moins 10 cycles de calculs.
Toutefois, comme le souligne le spécialiste français de la relativité générale Luc Blanchet, il est peu probable que cette orbite soit vraiment stable sur des périodes infinies car les pertes d'énergie sous forme d'ondes gravitationnellesondes gravitationnelles, que la théorie prédit à un ordre d'approximation plus élevé, devraient finir par modifier la forme de celle-ci.