Le rugby et les mathématiques

Pour transformer cet essai, le buteur doit poser le ballonballon sur la ligne passant par le point précis où l'essai a été marqué et perpendiculaire à la ligne de but, donc parallèle à la ligne de touche. Où placer le ballon sur cette ligne pour que la transformation soit la plus facile possible ?

Sortie de ruck. © Pierre Selim, Wikimedia commons, CC by 03

Si l'essai a été marqué entre les poteaux, le problème est relativement simple à condition de se placer assez loin pour passer au-dessus de la barre transversale et se mettre à l'abri de la charge de l'équipe adverse. Tout change si l'essai a été marqué hors des poteaux. Déplaçons un point sur cette ligne. L'angle sous lequel on voit les buts depuis ce point augmente quand on s'éloigne de la ligne de but pour passer par un maximum, puis diminuer. C'est en ce point où l'angle est maximal qu'il convient de placer le ballon.

Évolution de l’angle. Sur la figure, il est maximal en B. © Hervé Lehning, tous droits réservés
 

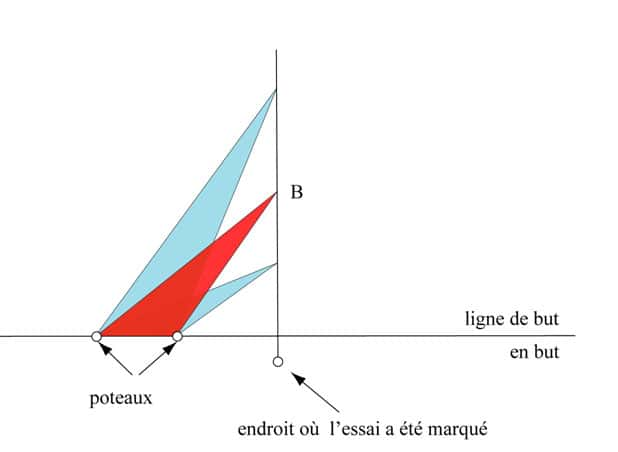
Quand nous faisons varier l'endroit où l'essai a été marqué, le point où l'angle est maximal décrit une courbe, qui se trouve être une hyperbole, ou plutôt un morceau d'hyperbole.

L’hyperbole de la transformation. © Hervé Lehning, tous droits réservés

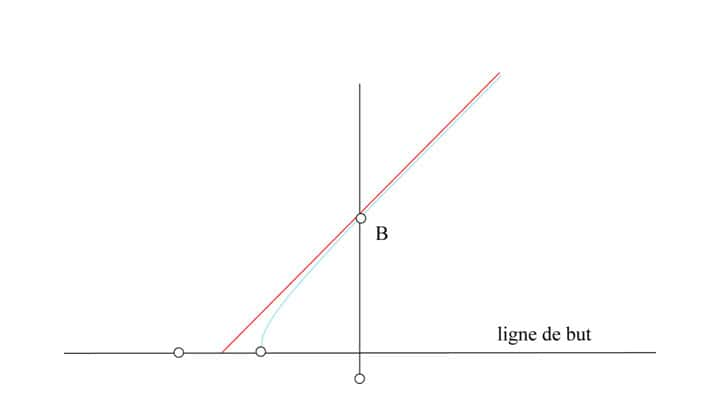
Bien entendu, on imagine mal le buteur tracer une hyperbole sur le terrain pour transformer son essai. Comme le montre la figure l'hyperbole de la transformation, cette hyperbole se confond vite avec deux droites, ses asymptotes. Ce sont les droites passant par le centre des poteaux, inclinées de ± 45 degrés. Pour trouver le point idéal, le buteur se déplace donc sur la ligne de transformation de la distance séparant le milieu des poteaux au point de la ligne de but où l'essai a été transformé.