au sommaire
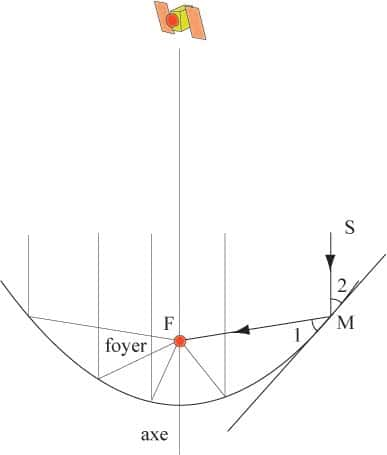
Pour commencer, les axes des paraboles doivent être orientés dans la direction du satellite, ce qui est fait par l'installateur une fois pour toutes. Les signaux SM venus du satellite S sont réfléchis en chaque point M de la parabole de sorte que les angles 1 et 2 (sur la figure) sont égaux.
La propriété géométrique essentielle de la parabole est que ce rayon réfléchi passe par un point fixe F, appelé le foyer de la parabole. Ceci étant vrai pour tout M, les signaux issus du satellite sont focalisés au foyer F.
© Hervé Lehning
Comment ne pas perdre le nord en ville ?
Les axes des paraboles sont orientés vers un point de l'équateuréquateur. Dans les latitudeslatitudes comme celles de la France, les paraboles désignent grossièrement le sud... ce qui donne une façon de s'orienter en regardant les paraboles sur les toitstoits.
Hervé Lehning
En savoir plus sur Hervé Lehning
Normalien et agrégé de mathématiques, Hervé Lehning a enseigné sa discipline une bonne quarantaine d'années. Fou de cryptographie, membre de l'Association des réservistes du chiffre et de la sécurité de l'information, il a en particulier percé les secrets de la boîte à chiffrer d'Henri II.
- Son blog MATH'MONDE sur Futura
- Le dernier livre d'Hervé Lehning :
À découvrir également : L'univers des codes secrets de l'Antiquité à Internet paru en 2012 chez Ixelles.