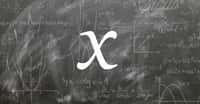Décomposer un nombre en la somme de trois cubes, ce n’est pas toujours évident. Mais les mathématiciens étaient déjà parvenus à trouver des solutions pour tous les entiers inférieurs à 100. Sauf 42. C’est désormais chose faite.

au sommaire

    Cela vous intéressera aussi

    [EN VIDÉO] Le monde est-il écrit en langage mathématique ? La nature est un livre écrit en langage mathématique, dont les lettres sont des triangles,...

    C'est en 1954 qu'a été posé le problème des trois cubes de la façon suivante : tout nombre entier peut-il s'exprimer comme la somme de trois entiers relatifs élevés au cube ? Ou, dans une écriture plus mathématique, comment trouver x, y et z avec k compris entre 1 et 100 dans l'équationéquation suivante : x3+y3+z3=k.

    Les solutions les plus évidentes ont rapidement été trouvées par les chercheurs. Et peu à peu, toutes les valeurs de k ont pu être résolues ou démontrées insolubles. Seules deux valeurs de k continuaient de donner du fil à retordre aux mathématiciens. En début d'année, le professeur Andrew Booker, de l'université de Bristol (Royaume-Uni), a résolu l'énigme pour k=33 en s'appuyant sur des semaines de temps d'un supercalculateur. Mais pour résoudre l'équation pour k=42, l'opération s'annonçait encore plus délicate.

    Entre 1 et 100, il existe 22 nombres entiers qui ne peuvent pas s’écrire comme la somme de trois entiers relatifs élevés au cube. Parmi eux, 4, 5, 13 et 14. © Chopard Photography, Fotolia
    Entre 1 et 100, il existe 22 nombres entiers qui ne peuvent pas s’écrire comme la somme de trois entiers relatifs élevés au cube. Parmi eux, 4, 5, 13 et 14. © Chopard Photography, Fotolia

    Des solutions hautement improbables

    Alors Andrew Booker a fait appel à Charity Engine, une sorte d'ordinateurordinateur mondial qui exploite la puissance de calcul inutilisée de plus de 500.000 PCPC. Une solution qui a tout de même nécessité plus d'un million d'heures de calcul pour en arriver aux valeurs suivantes : x = -80.538.738.812.075.974, y = 80.435.758.145.817.515 et z = 12.602.123.297.335.631.

    « Nous n'avions aucune certitude quant à ce que nous allions trouver. Un peu comme lorsque l'on essaie de prédire un séisme. Nous aurions aussi bien pu continuer à chercher cette solution pendant un siècle encore. Mais aujourd'hui, je me sens soulagé », indique Andrew Booker. Ne lui reste plus qu'à se pencher sur la dizaine de décompositions manquantes pour les k inférieurs à 1.000 !