au sommaire

L'univers de Gödel et la solution de Kerr
Considérons maintenant une autre étape vers la théorie moderne des voyages dans le temps et l'espace : l'univers de Gödel et la solution de Kerr.

Kurt Gödel et Einstein à Princeton. © Oskar Morgenstern, Institute of Advanced Study Archives
L'univers de Gödel
La généralisation dans le cadre de la RG de la solution newtonienne décrivant le champ de gravitation d'une étoile ne décrit avec celle de Schwarzschild qu'un corps dénué de rotation. Ce n'est pas très réaliste du point de vue de l'astronomie car les étoiles, tout comme les planètes, sont animées d'un mouvement de rotation.
Une des premières solutions décrivant le champ généré par un corps en rotation fut celle de Van Stockum, (Stockum, W. J. van (1937). The gravitational field of a distribution of particles rotating around an axis of symmetry. Proc. Roy. SocSoc. Edinburgh A 57: 135). L'histoire de son auteur vaut un roman à elle toute seule.
C'est aussi le premier exemple où l'on voit une connexion entre le voyage dans le temps et l'existence d'une rotation associée à l'espace-temps. Probablement inspiré par cette découverte, par de nombreuses discussions avec Albert EinsteinEinstein (dont il était le collègue et l'ami à Princeton) sur l'espace, le temps et leurs relations avec la physiquephysique et la philosophie, le grand logicien Kurt GödelKurt Gödel stupéfia le monde en 1949 en exhibant une solution des équationséquations d'Einstein décrivant un univers en rotation. Ce qu'elle avait d'étrange était qu'il existait à l'intérieur de celle-ci des trajectoires permettant à un voyageur de remonter dans son propre passé !
Comment cela est-il possible ?
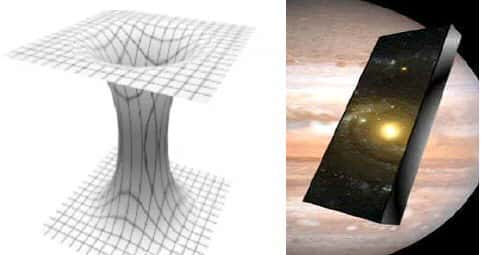
Il existe dans cette solution un axe de rotation privilégié dans l'univers, au fur et à mesure que l'on s'éloigne de cet axe la structure causale de l'espace-temps se modifie. Il existe toujours une vitessevitesse limite mais si l'on introduit un champ de cônescônes de lumièrelumière on s'aperçoit que ceux-ci basculent de plus en plus au fur et à mesure que l'on s'éloigne de l'axe, de telle sorte que la direction du futur pour un observateur à l'intérieur de son cône de lumière coïncide maintenant avec une trajectoire remontant dans le passé !
Un tel basculement des cônes de lumière est justement caractéristique du passage de la relativité restreinterelativité restreinte à la relativité généralerelativité générale, comme on l'a vu la métrique est alors dynamique.
C'est un phénomène de la plus haute importance, on le verra plus loin pour les trous noirstrous noirs ou la cosmologiecosmologie.

Extrait de Cern yellow report 91-06. © Ruth M. Williams
De cette façon, il existe dans la solution de Gödel un ensemble de trajectoires dites de genre temps closes qui, parcourues par un observateur à l'aide d'une fuséefusée, lui permettraient de remonter dans le temps. Dans cette solution de Gödel il est important de noter que seuls des voyages dans le passé sont admis, à part bien sûr les voyages habituels dans le futur comme les jumeaux de Langevin.

Le basculement des cônes de lumière dans l'univers de Gödel permet la formation de boucles temporelles selon certaines lignes d'univers (world-line) pour un voyageur. Extrait de Cern yellow report 91-06 © Ruth M. Williams
Une remarque intéressante, cette solution cosmologique décrit un univers sans singularité initiale.
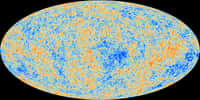
L'existence de boucles causales fermées du genre temps se trouve en fait étroitement liée à l'absence de singularités en général dans les solutions des équations d'Einstein. Autant prévenir tout de suite le lecteur, les données issues de l'observation du fond de rayonnement cosmologique n'indiquent aucun signe de rotation globale de l'univers.
La solution de Kerr
Dans le cadre d'une meilleure compréhension des solutions décrivant des objets astrophysiquesastrophysiques réalistes, le début des années 1960 est marqué par une double révolution théorique.
L'introduction par Kruskal d'un système de coordonnées permettant de décrire complètement et de façon plus précise la structure géométrique et topologique de la solution de Schwarzschild et la découverte de la solution de Kerr.
Diagramme de Kruskal
En utilisant le système de coordonnées introduit par Eddington et retrouvé par Finkelstein, Martin Kruskal fut capable de résoudre les problèmes liés à la description de la structure de l'espace-temps lorsqu'on s'aventure sous la surface délimitée par le rayon de Schwarzschildrayon de Schwarzschild. Encore une fois, c'est la considération de trajectoires de rayons lumineux qui fut la clé pour surmonter la difficulté. On pouvait désormais représenter la géométrie passée et future de l'espace-temps de cette solution par les diagrammes ci-dessous.
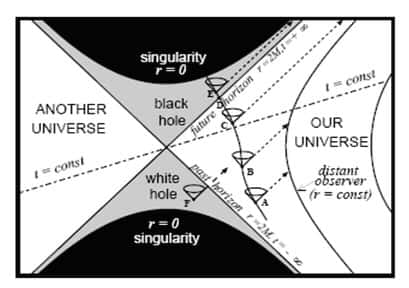
Diagrammes de la géométrie passée et future. Voir ci-dessous pour plus de détail. Extrait de Jean-Pierre Luminet - Black Holes : A General Introduction. © Jean-Pierre Luminet
Les deux cônes définissent le futur et le passé de l'horizon des événementshorizon des événements du trou noir, les droites avec tirets et points définissent des coupes à temps constant de l'espace-temps et les courbes verticales ressemblant à des paraboles correspondent à des sphères de rayon constant dans le temps entourant le trou noir. Comme les équations d'Einstein sont symétriques dans le temps, le cône du haut correspond à un trou noir dans lequel tout ne peut que rentrer sans jamais sortir ; alors que le cône du bas correspond, par renversement du temps, à une solution dite de trou blanc ou encore de fontaine blanche. Ici tout sort sans jamais pouvoir entrer. La région à gauche est en relation directe avec un autre feuillet d'univers dans un cas de type pont d'Einstein-Rosen ou trou de ver de Misner. Les régions en noir sont celles « étalées » par le système de coordonnées où la singularité finale se trouve, l'espace-temps s'y anéantit !
Le nouveau système de coordonnées allait se trouver précieux pour l'étude de la solution décrivant un astreastre en rotation trouvée par la mathématicienmathématicien Néo-Zélandais Roy Kerr. Son étude intensive fut l'œuvre de Brandon Carter et de Subrahmanian Chandrasekhar. Cette solution ne décrit exactement que ce qu'on appellera plus tard un trou noir et personne n'a réussi à démontrer qu'il s'agissait de la solution exacte décrivant la géométrie extérieure d'une étoile simple en rotation.

Roy Kerr - À gauche Roy Kerr, à droite Brandon Carter. © DR
La métrique décrivant un trou noir en rotation trouvée par Kerr peut s'écrire de la façon suivante (coordonnées de Boyer-Lindquist, en posant, G = c = 1) :
ou
Selon les valeurs respectives de M et a, on peut obtenir des boucles du genre temps violant les exigences de la causalité dans le cadre de cette géométrie de l'espace-temps. On ne sera pas surpris que a soit directement lié au moment cinétiquemoment cinétique J du trou noir en rotation.
Le trou noir de Kerrtrou noir de Kerr possède, en plus d'un horizon des événements (event horizon), une ergoshère de forme ellipsoïdale. Tout corps en chute radiale traversant cette région, dite de frame dragging (en français entraînement des référentielsréférentiels), se verra irrésistiblement entraîné par la rotation de l'espace-temps induit par le trou noir. Il possédera donc une composante tangentielle de vitesse et l'on se retrouvera dans une situation parente (mais pas identique) à celle de l'univers de Gödel.
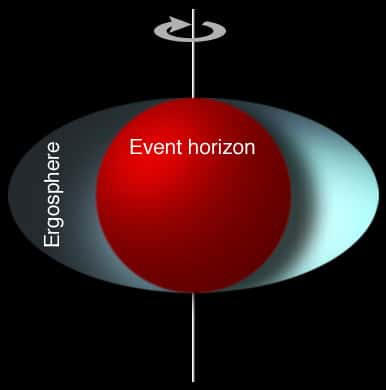
Un schéma montrant la différence entre l'horizon des événements (sphérique) et l'ergosphère (ellipsoïdale) d'un trou noir de Kerr. © MesserWoland, Wikipedia
Combinés à la découverte récente des quasars (interprétables à l'époque comme des étoiles supermassives nécessairement décrites par la relativité générale), à la détection en 1965 du rayonnement fossilerayonnement fossile prédit par les modèles cosmologiques de type Big BangBig Bang et enfin celle des pulsarspulsars en 1967 (confirmant l'existence d'étoiles à neutronsétoiles à neutrons), ces nouveaux outils théoriques allaient entraîner une brutale accélération du développement de l'astrophysique relativiste et une renaissance des recherches en relativité générale, éclipsée largement à partir des années 1930 par les succès de la physique quantiquephysique quantique.