au sommaire
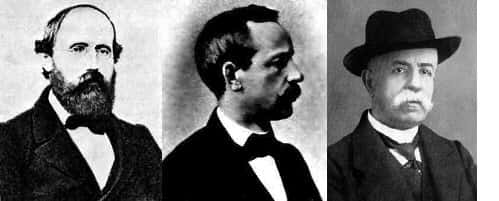
La relativité générale d'Einstein
Voici quelques rappels, très utiles, sur la théorie de la relativité générale. Ils permettront de poser les concepts de base.
De gauche à droite, Riemann, Christoffel, Ricci-Curbastro, les mathématiciens ayant développé les outils de géométrie non euclidienne nécessaires à la formulation de la relativité générale. © DR
Il est vivement conseillé au lecteur de se référer constamment au dossier de Futura-Sciences pour des explications plus détaillées, voir de le lire comme préambule indispensable avant de continuer pour qui n'a jamais rien lu sur la relativité générale (en abrégé RG).
Gravitation et relativité restreinte
EinsteinEinstein fut assez vite confronté au problème de la réconciliation entre la théorie de la gravitation de Newton et sa propre théorie de la relativité restreinte.
Laplace avait montré que l'influence de la gravitation devait se propager au moins plusieurs millions de fois plus vite que la lumière pour correspondre aux orbites des planètes observées dans le Système solaireSystème solaire.
En outre, la théorie d'Einstein traite de la description des mouvementsmouvements dans des référentielsréférentiels sans accélération. Miraculeusement ces deux problèmes sont liés et peuvent être surmontés par la remarque incroyablement simple suivante : les massesmasses inertes et gravitationnelles des corps sont identiques. Qu'est-ce que cela signifie ?
La masse inerte est le coefficient qui intervient dans la loi de Newton liantliant l'accélération d'un corps à la force qu'il subit, celle dite gravitationnelle est liée à l'estimation de l'intensité de la force qu'un corps subit dans un champ de gravitation. Cela est d'autant plus troublant que dans le cas d'une force électrique ou magnétique c'est la charge qui apparaît. On soupçonne donc un lien entre lois de la mécanique et loi du champ de gravitation.
Une applicationapplication frappante de cette égalité est aujourd'hui les expériences dans des avions momentanément en chute libre. À l'intérieur de l'avion, tous les corps chutant à la même vitessevitesse par rapport à la Terre se mettent à flotter les uns par rapport aux autres.
Localement on peut donc trouver un référentiel dans lequel les effets du champ de gravitation s'annulent !
Inversement on peut trouver un référentiel accéléré tel qu'un observateur puisse se croire immobile mais soumis à un champ de gravitation. Le pas fondamental suivant pour atteindre les fondements de la relativité générale consiste à regarder ce qui se passe lorsqu'on essaie d'appliquer la relativité restreinte à des corps accélérés. Généralement on considère le cas d'un disque en rotation uniforme.
Chaque point le long d'un rayon est soumis à une vitesse v de plus en plus importante lorsqu'on s'éloigne du centre du disque. Une horloge en chacun de ceux-ci aura donc un décalage de plus en plus prononcé au fur et à mesure qu'on s'éloigne de ce centre. En outre la mesure de la circonférence du disque indique en raison de la contraction des longueurs que celle-ci n'apparaît pas comme vérifiant la relation C=2πR.
La géométrie spatiale n'est donc plus euclidienne pour certains observateurs et ceci en relation avec le fait qu'on est en présence de mouvements accélérés.
Or, on l'a vu, une accélération dans un référentiel est interprétable localement comme la présence d'un champ de gravitation. On vient donc de mettre en évidence un lien entre gravitation et géométrie de l'espace. Einstein en conclut que les phénomènes gravitationnels devaient être en toute généralité liés à une géométrie non euclidienne de l'espace-tempsespace-temps et pas seulement de l'espace, sans quoi on aurait une contradiction avec le concept même d'espace-temps en régime sans gravitation.
La théorie des espaces courbes à N dimensions
C'est tout naturellement qu'il fut conduit à utiliser la théorie générale des espaces courbes à N dimensions introduite au XIXe siècle par Riemann.
Dans ceux-ci, la géométrie n'est plus euclidienne, la somme des angles d'un triangle ne fait plus 180° et la circonférence d'un cercle n'est plus égale à 2πR. C'est ce qu'on peut facilement constater avec des figures géométriques sur les surfaces ci-dessous. Possédant une courbure respectivement positive (comme pour une sphère), ou négative (comme une selle de cheval), on ne peut les appliquer sur un plan sans déchirures ou sans les friper.

Une surface à courbure positive à gauche ne peut pas s'aplatir sur un plan sans se déchirer. Une surface à courbure négative ne peut pas s'aplatir sans se friper. Extrait de Cern yellow report 91-06. © Ruth M. Williams
La métrique précédente apparaissant dans l'intervalle sous forme infinitésimale
se trouvera généralisée en
et sera décrite par un tenseurtenseur qui bien évidemment se réduit au précédent lorsque l'espace est plat.
Son introduction remonte aux investigations de Gauss au début du XIXe siècle sur la géométrie des surfaces courbes, une évidente conséquence de ses travaux sur la géodésiegéodésie.
Remarquons aussi qu'il existe le concept d'action et de réaction en physiquephysique Newtonienne. Les forces centrifugesforces centrifuges sont liées à des référentiels accélérés et par le principe d'équivalence interprétable comme des forces gravitationnellesforces gravitationnelles, à quoi pourrait donc correspondre la réaction de la matièrematière à une accélération par changement de référentiel ?
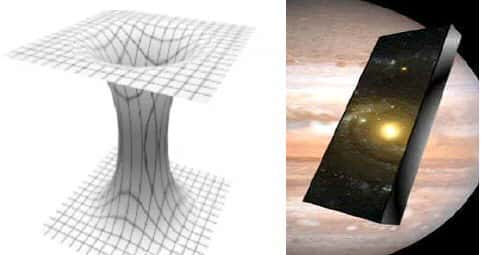
Dans le contexte précédent une réponse émerge naturellement, c'est l'espace-temps lui-même qui doit se déformer !
On retrouve d'une autre façon une liaison entre un espace-temps à géométrie variable et le champ de gravitation.
Comme une distribution de matière est liée à une distribution d'énergieénergie, qu'en outre la matière génère un champ de gravitation, on en déduit qu'il doit exister des équationséquations généralisant celles de la gravitation Newtonienne et connectant distributions de matière/énergie et géométrie de l'espace-temps.
L'exploit principal d'Einstein fut d'obtenir ces équations, elles s'écrivent :
Le membre de gauche contient la géométrie de l'espace-temps, on y trouve le tenseur métrique ainsi que ses dérivées spatiales et temporelles. Il s'agit du fameux tenseur d'Einstein construit à l'aide du tenseur de courbure de Riemann-Christoffel
qui une fois contracté (par sommation selon Einstein de deux indices, cf. précédemment) donne le tenseur de Ricci à deux indices.
Le membre de droite contient, par exemple, l'énergie et la quantité de mouvementsquantité de mouvements attribuées à une distribution de matière ou de champ électromagnétiquechamp électromagnétique. Cela est contenu dans le tenseur T à deux indices que l'on appelle le tenseur d'impulsion-énergie. La métrique de l'espace-temps devient donc bien un objet dynamique déterminé par la distribution et le mouvement de la matière/énergie.
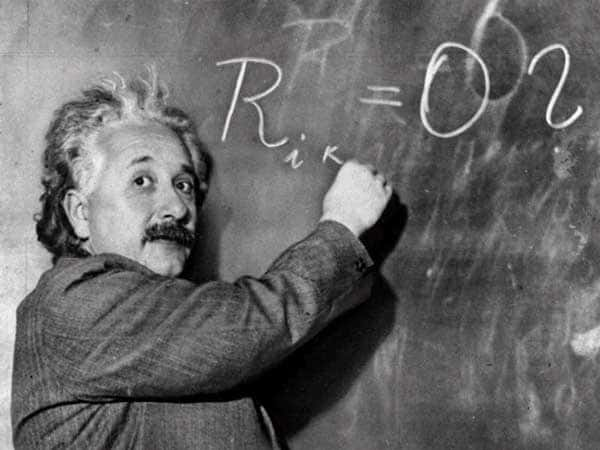
Albert Einstein devant ses équations de la gravitation dans le vide. Elles se réduisent à la nullité du tenseur de Ricci. © DR
La géodésique
Tournons-nous maintenant vers un autre concept important en relativité générale.
La généralisation d'une ligne droite en espace-temps courbe est ce qu'on appelle une géodésique. Ainsi sur la surface de la Terre, si l'on part de l'équateuréquateur pour atteindre le pôle en suivant la longitudelongitude coupant le point de départpoint de départ ce sera précisément une telle courbe.
De manière générale c'est la courbe de longueur minimale entre deux points sur une surface. Selon GaliléeGalilée et Newton un corps en l'absence de force est au repos ou se déplace selon une trajectoire rectiligne uniforme, une droite.
La généralisation en espace-temps courbe est donc bien une géodésique et si en physique newtonienne une force se décrit par un écart à une trajectoire rectiligne uniforme alors, dans ce cadre, la gravitation selon Einstein n'est plus une force au sens de Newton car les corps ne font que suivre des trajectoires « droites » dans l'espace-temps sous l'action de la gravitation.
C'est ce qui est illustré par les schémas ci-dessous pour le mouvement des planètes autour du SoleilSoleil.

Une particule cherchant à se déplacer selon la ligne la plus droite possible peut emprunter une tangente à un cercle centré sur le puits à gauche. Atteignant le cercle, elle se trouvera piégée en orbite en suivant la courbe la plus droite, c'est à dire ici précisément ce cercle. À droite, un bloc d'espace-temps avec la trajectoire dans le temps d'un astre fixe et un objet tournant autour de lui. Cern yellow report 91-06. © Ruth M. Williams
La théorie du potentiel newtonien pour les étoiles
On s'attend bien sûr à une modification de la théorie du mouvement des planètes.
Comme l'a démontré Karl Schwarzschild, il est possible de trouver une solution généralisant celle de la théorie du potentiel newtonien pour un astreastre.

Karl Schwarzschild (1873-1916). © DR
À l'extérieur d'une étoileétoile parfaitement sphérique, de masse M et sans rotation (on parle de cas statique), la géométrie de l'espace-temps est décrite par :
Il existe aussi une solution interne que l'on écrira simplement sous la forme ci-dessous :
Si l'on considère une sphère de rayon r à l'intérieur de l'astre, elle contiendra une masse M(r). Ce qui explique son apparition dans l'intervalle d'espace-temps précédent.
Ces solutions étaient en fait des mines d'or dont les richesses mettraient des dizaines d'années à se révéler. Le premier signal allait venir d'Einstein en 1935.
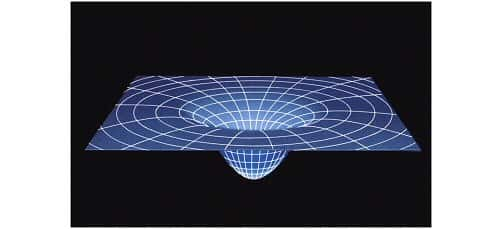
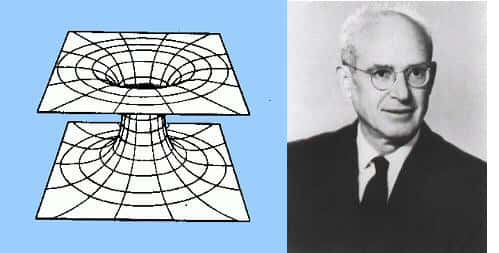
Diagramme de plongement 2D de la solution de Schwarzschild. © DR
Entretemps, on avait remarqué deux problèmes. Lorsque la masse d'une étoile décrite par les solutions précédentes passait sous le rayon Rs= 2GM/c2 (ou 2GM lorsque l'on pose c=1 dans le système d'unités habituellement utilisé), dit rayon de Schwarzschildrayon de Schwarzschild, que se passerait-il ? Déjà la première solution dans le vide semble devenir pathologiquepathologique lorsque r=Rs car on obtient l'infini pour le second terme de la métrique.
De même, en r=0 et toujours dans le premier cas, on trouve que la courbure de l'espace-temps devient infinie. C'est là qu'on se met à parler de singularité pour la géométrie de l'espace-temps en ce point où les équations d'Einstein et la structure de l'espace-temps s'effondrent.