Mathématiques : le secret d'un ballon qui roule

Connaissez-vous la relation d'Euler f + s - a = 2 ? Elle s'applique à tout solide dans l'espace, par exemple le dé. Il a 6 faces (f), 8 sommets (s), 12 arêtes (a). On retrouve bien 6 + 8 - 12 = 2. Cette relation est également vraie pour les quatre autres solides de Platon, le tétraèdre (4 faces triangles équilatéraux, 4 sommets, 6 arêtes), l'octaèdre (8 faces triangles équilatéraux), le dodécaèdre (12 faces pentagonales, 20 sommets, 30 arêtes) et enfin l'icosaèdre (20 faces triangles équilatéraux, 12 sommets, 30 arêtes).

Elle s'applique aussi... au ballonballon de football qui est, lui aussi, un solide dans l'espace. Comment est construit un ballon de foot ? Ses faces sont-elles des triangles (3 côtés), des carrés (4 côtés), des pentagones (5 côtés), des hexagones (6 côtés) ? Vous avez sans doute une petite idée, on peut aussi s'aider avec l'image. Excluons déjà les deux premiers : difficile de faire rouler le ballon avec des triangles ou des carrés ! Voyons les deux derniers. La géométrie nous démontre que l'on ne peut refermer un solide sur lui-même en partant uniquement d'hexagones. Vous ne pourriez coudre votre ballon... C'est aussi pour cette raison que je ne vous propose pas de fabriquer le ballon avec des polygones à plus de six côtés (heptagone, octogone...).

Le secret d'un ballon qui roule

Donc on ne peut pas prendre uniquement des hexagones : le ballon roulerait bien, mais il ne peut être construit ! Si l'on ne prend que des pentagones, on se retrouve justement avec un des solides réguliers, le dodécaèdre (12 faces pentagonales) : pas mal mais il ne roule pas terrible. Peut mieux faire.

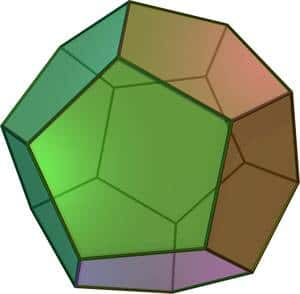
Le dodécaèdre ? Il a 12 faces pentagonales. Pas terrible pour rouler.
© Commons

La solution optimale se situe entre les deux : pas uniquement des faces hexagonales (couture impossible) et pas uniquement des faces pentagonales (ne roule pas bien).

En fait, le ballon de football est composé de 20 hexagones (les faces blanches) et de 12 pentagones (les faces noires) : le saviez-vous ? Euler vérifie sa relation sur le ballon : 32 faces + 60 sommets - 90 arêtes = 2. Vérifiez vous-même en comptant sur un vrai ballon !

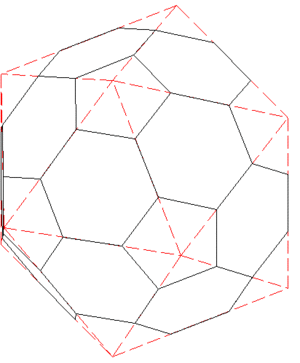
Le ballon de foot est un icosaèdre tronqué : les 12 sommets sont coupés, se transformant en 12 pentagones ; les 20 faces triangulaires deviennent ainsi 20 hexagones.

Pour ceux qui veulent aller plus loin : en fait le ballon de foot est un icosaèdre tronqué, c'est-à-dire le plus grand solide de Platon (pour avoir la plus grande surface de roulage régulière possible) auquel on aurait rogné les pointes pour le faire rouler. Chacun des 12 sommets est rasé, transformé en pentagone (il reste les 20 faces initiales de l'icomachin - de triangles, elles deviennent hexagones - et les 12 sommets sont transformés en 12 faces pentagonales).

Euler, paraphrasant GaliléeGalilée, pourrait nous dire de son ballon : « Et pourtant, il tourne ! ».