au sommaire
Maths : transport au moindre coût
Je travaille sur le transport optimal, un domaine à la fois ancien (né il y a plus de 200 ans), et nouveau, puisque ses ramifications n'ont jamais été aussi nombreuses qu'aujourd'hui. En suivant quelques-unes de ses péregrinations, nous verrons comment la magie des mathématiques peut s'approprier, mélanger et métamorphoser des sujets venus d'horizons divers.
Pour résumer en un slogan la problématique du transport optimal : il s'agit de transporter des ressources au moindre coût. Ici les ressources sont des biens que l'on doit acheminer depuis les producteurs jusqu'aux consommateurs.
Pour prendre un exemple concret et agréable, supposons que ces ressources soient des croissants (cuits du matin, bien croustillants !).
Nous avons donc des boulangeries, appelons-les B1, B2, B3, qui chaque matin produisent des croissants, et il faut acheminer ces croissants vers des cafés que nous appellerons C1, C2, C3. Imaginons également que dans un effort louable, toutes ces boulangeries et ces cafés ont décidé de mettre leurs ressources en commun pour être plus efficaces (une sorte de grand consortium où personne ne se fait de concurrence), et réfléchissent ensemble à agir selon l'intérêt commun.
On sait à l'avance combien de croissants sont produits dans chaque boulangerie, et combien devraient être consommés dans chaque café : par exemple la boulangerie B1 produit 5 paniers, le café C1 veut 3 paniers, le café C2 en veut 7, etc...
Le problème est de décider où vont être acheminés les croissants des uns et des autres : vaut-il mieux envoyer toute la production de la boulangerie B1dans le café C2, ou bien la séparer en deux parties et envoyer un morceau en C1, un morceau en C2, etc...? Les solutions ne sont pas équivalentes car le transport se paie plus ou moins cher : si une boulangerie fournit un café à l'autre bout de la ville, le déplacement sera plus onéreux que si c'est un café tout proche.
Le problème de transport optimal consiste à faire les appariements en minimisant le coût de transport total (par exemple la distance totale parcourue par les coursiers).

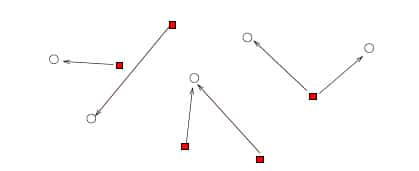
Fig. 1. Les carrés représentent les boulangeries, les cercles blancs les cafés. Les flèches indiquent où sont acheminés les croissants : ces flèches sont les inconnues du problème de transport optimal.
Dans la suite, je vais préciser ce problème, évoquer brièvement son histoire, et des directions de recherche qui lui sont liées.
un domaine à la fois ancien (né il y a plus de 200 ans), et nouveau, puisque ses ramifications n'ont jamais été aussi nombreuses qu'aujourd'hui.