au sommaire
L'autre type de nombres infinis de Cantor (avec les cardinaux, voir page 4), les ordinaux, sert à mesurer la taille des ensembles lorsque leurs éléments sont ordonnés selon un bon ordre (un ordre tel que toute partie de l'ensemble possède un plus petit élément). Au-delà des ordinaux finis, qu'on assimile aux nombres entiers, il y a ω, le premier ordinal transfini, puis ω+1, ω+2, etc., qu'on obtient en ajoutant des unités une à une à ω. Plus loin encore, on trouve 2ω, 2ω+1... puis ω2, ωω, etc.
Formule mathématiques. © Dimitrios Vrettos, CC BY 3.0
Cantor découvre alors un problème qui finalement se révélera d'une difficulté qu'aujourd'hui encore nous n'avons pas totalement maîtrisée : l'hypothèse du continu.

Pour éviter le paradoxe du menteur, on s’interdit les phrases autoréférentes. Mais ce n’est pas aussi simple avec l’infini… © Belin
Le cardinal de l'ensemble des nombres réels ℝ, ce qu'on appelle le continu et qui est mesuré par , est strictement plus grand que le cardinal des entiers (appelé infini dénombrable et mesuré, nous l'avons dit, par
)). Mais y a-t-il un autre cardinal entre les deux ? L'hypothèse du continu est l'affirmation qu'entre ces deux tailles d'ensembles infinis,
et
, il n'y en a pas d'autres. Comme Cantor désigne par
le plus petit des cardinaux plus grands que
, l'hypothèse du continu est simplement l'affirmation
=
(l'hypothèse généralisée du continu est l'affirmation que
=
pour tout s).
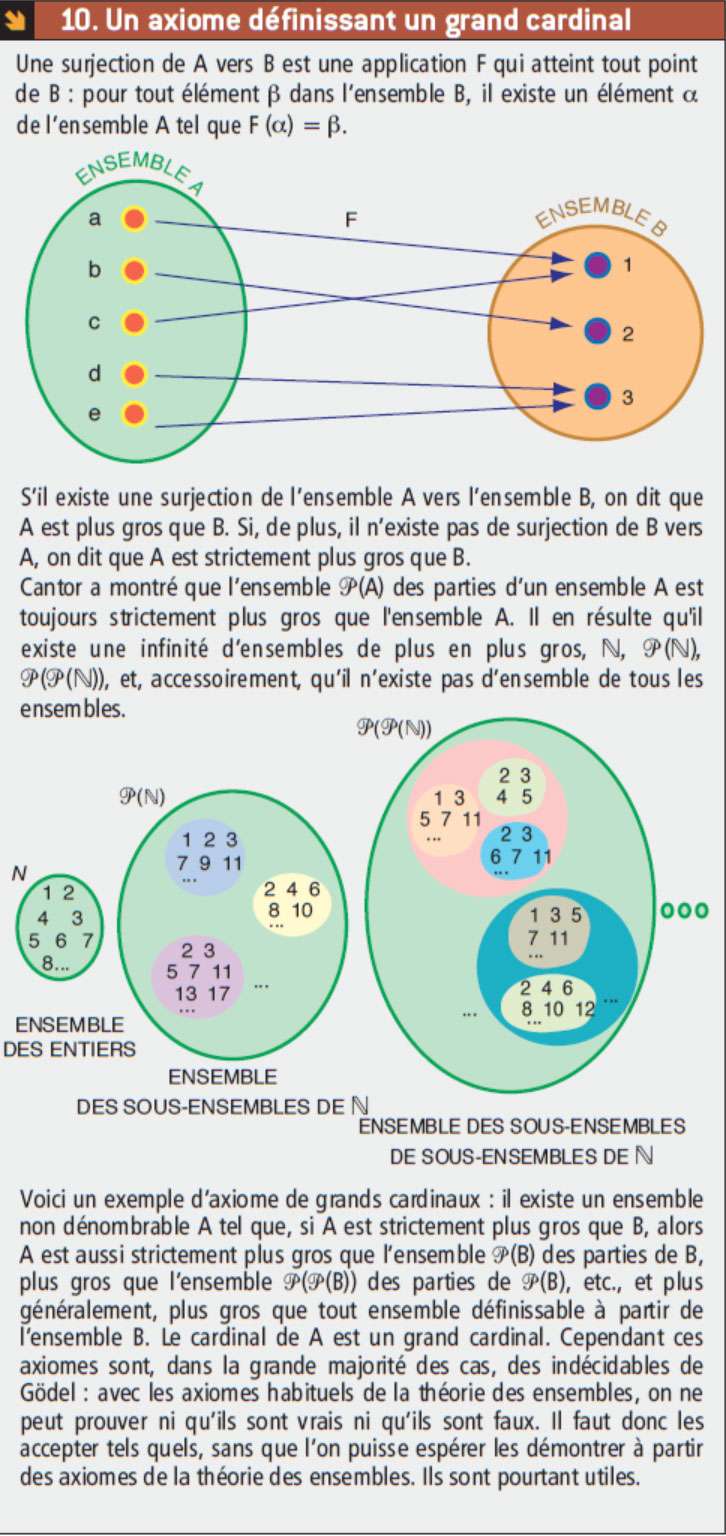
Un exemple illustré de grand cardinal. Cantor a montré que l’ensemble P(A) des parties d’un ensemble A est toujours strictement plus gros que l’ensemble A. © Belin
Deux situations sont envisageables : soit il n'y a pas d'autres tailles infinies entre ℕ et ℝ, ce qui est équivalent à dire que « tout sous-ensemble infini de ℝ peut être mis en bijection avec ℕ ou avec ℝ » (c'est là un énoncé simple et, en apparence, très concret) ; soit il y en a d'autres et alors il faudrait savoir combien et comment on les obtient. Nul ne peut prétendre disposer d'une idée claire des nombres réels s'il n'a une réponse précise au problème de l'hypothèse du continu. Cantor s'épuisera à le résoudre et n'y réussira pas, bien qu'il ait parfois pensé, à tort, avoir résolu la question.