au sommaire
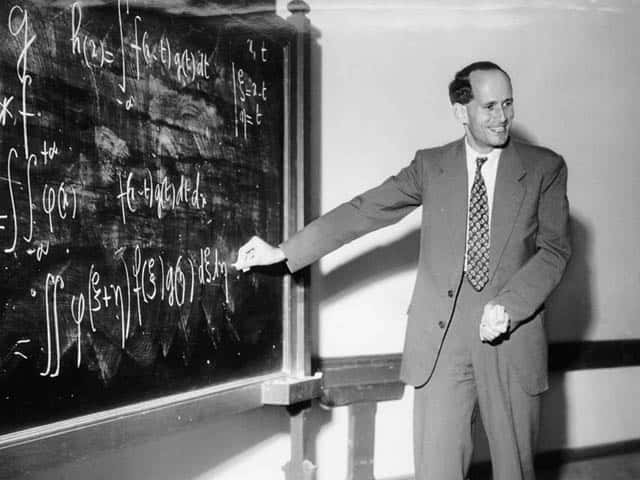
Les distributions, ou comment donner un sens à des objets qui n'en ont pas
On vient de parler de fonctions, au sens élémentaire. Dans les premières décennies du XXe siècle, la nécessité est apparue de généraliser cette notion ; ainsi naquit la théorie des distributions, ou fonctions généralisées, dont nous sommes redevables à Laurent SchwartzLaurent Schwartz, Guelfand et Chilov, mais l'un des pionniers (malgré lui ?) fut Dirac, physicienphysicien audacieux sur tous les plans, notamment par l'introduction de sa fonction qui, pour n'en être pas une, lui attira bien des critiques, des foudresfoudres, voire des sarcasmes.
De quoi s'agit-il ? Justement, de donner la rigueur souhaitable à des objets d'apparence mal fichus, que les physiciens manipulent sans vergogne et sans prendre la peine (honte à eux !) de préciser qu'ils se réfèrent implicitement aux bonnes échelles et que, relativement à celles-ci, toutes les opérations techniques sont physiquement justifiées (et justifiables). Pour les mathématiciensmathématiciens, non asservis à des échelles qui pour eux n'existent pas, il fallait mettre de l'ordre -- et, bien sûr, ils l'ont fait.
Comme toujours, cette remise en ordre suivant les canons de la rigueur a été d'une grande féconditéfécondité, ne se bornant pas à rassurer les physiciens (qui n'avaient pas besoin de l'être) que, tout compte fait, ils n'avaient pas perdu la tête -- d'ailleurs, les succès des théories construites par des moyens suspects étaient là pour en apporter la preuve. Par ses développements, la théorie des distributions a élargi le champ de la recherche et, sur un plan plus pragmatique et en juste retour des choses, a permis aux physiciens de se sortir de difficultés techniques dont ils ne savaient pas se dépatouiller.
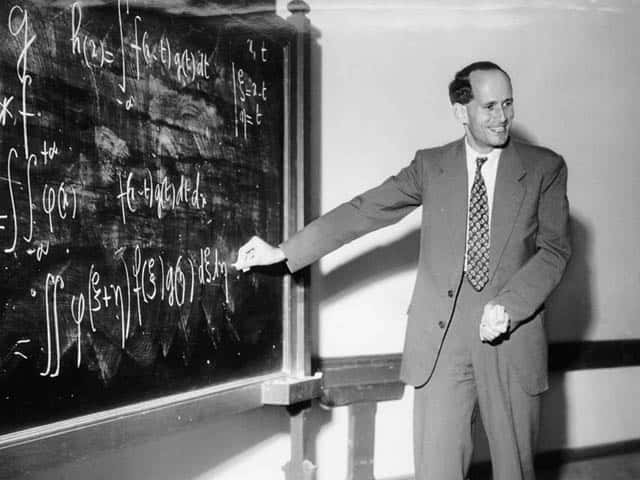
Médaille Fields de mathématique, le grand mathématicien Laurent Schwartz (1915-2002) était aussi très engagé, et il a été membre du Tribunal Russell. Ses talents d'enseignants étaient légendaires, comme en témoigne son cours d'analyse de l'École polytechnique. Il était un des membres de Bourbaki. © École polytechnique
Il n'est pas possible d'en dire beaucoup plus avec les mots du langage commun, mais un exemple élémentaire permettra de comprendre (un peu) de quoi il s'agit, même s'il est (forcément) un tantinet technique. Mettez l'intégrale suivante :
sous le neznez d'un étudiant de première année et demandez-lui de la calculer. S'il a bien appris son cours, la réponse sera immédiate : pas question de la calculer, puisqu'elle n'existe pas. Et si vous en semblez surpris, on vous expliquera que la fonction à intégrer se comporte trop mal à l'origine (en x = 0), et donc n'est pas intégrable. Rien à rétorquer, sauf que la théorie des distributions vous dit quoi faire en pareil cas et, pour une fois, ne se borne pas à cela : en prime, elle vous donne la valeur de l'intégrale, qui est... . Le même étudiant vous dira alors que l'on est en pleine folie : non seulement on se permet de donner une certaine valeur à une intégrale qui n'existe pas mais encore cette valeur est négative, alors que la fonction à intégrer est partout positive.
Bien sûr, il n'y a rien de délirant là-dedans, tout est parfaitement correct. La seule chose que l'on peut faire, c'est juste ajouter des guillemets à l'égalité :
pour marquer le fait que l'égalité doit être comprise dans un sens généralisé et que, en définitive, tout le monde a raison. Tout comme Ramanujan n'avait pas tort d'écrire :
(une somme en nombre infini de nombres tous positifs et qui est négative, une horreur), son génie l'autorisant à omettre des guillemets sans doute pour lui totalement superflus, mais l'exposant ainsi aux critiques acerbes de Hill -- justifiées, pas justifiées ?
La genèse et les développements de la théorie des distributions constituent un nouvel exemple de l'enrichissement permanent que s'apportent mutuellement mathématiques et physique. Les élucubrations (?) de Dirac ont conduit les mathématiciens, par nature attachés à la plus grande rigueur, à aller au-delà de leurs premières (mauvaises) impressions. L'arsenal conceptuel et technique ainsi constitué a fourni de nouvelles armes et de nouveaux outils aux physiciens pour se tirer d'affaire dans d'autres situations où l'impasse semblait sans issue.
Ce n'était pas la première fois, il y en aura d'autres.