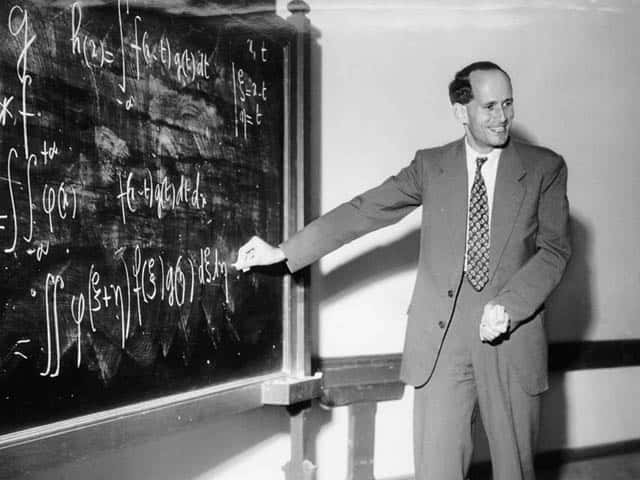au sommaire
Une autre invraisemblance de la théorie quantique est la négation de l'existence d'une trajectoire pour une particule (l'expérience des fentes d'Young est là pour s'en convaincre) : une particule ne se déplace pas dans l'espace comme le sens commun semble l'imposer, c'est-à-dire en suivant une certaine ligne dans l'espace au cours du temps.

Deux des pères fondateurs de la théorie quantique et de son interprétation physique, Werner Heisenberg (à gauche) et Niels Bohr (à droite). Ils étaient très conscients du fait que l'on ne pouvait pas attribuer aux quanta de matière et de lumière une trajectoire dans l'espace et dans le temps dans un sens classique. © AIP, Niels Bohr Library
En effet, pour construire celle-ci, il faut définir avec une précision totale et au même instant un point (qui donne la position) et en ce point une tangente (qui donne la vitesse) ; Heisenberg, à travers ses illustrissimes relations dites d'incertitude, nous a appris que pour une particule très petite, c'est un leurre.
© De Boeck
Pas de trajectoire, dites-vous, et pourtant, pour un objet macroscopique, on la voit, la trajectoire. Et d'ailleurs, on la voit aussi lorsqu'une particule chargée traverse une chambre de Wilson. En fait, dans ce dernier cas, on croit la voir, mais en fait, il ne s'agit que d'une trace formée de petites gouttes condensées, dont la taille est de l'ordre du micron ; aussi minuscules soient-elles (pour l'œilœil), elles sont gigantesques par rapport à la taille (présumée) de la particule que l'on a « vue » se promener. S'il s'agit d'un proton baladeur, dont le rayon est inférieur à un millionième de milliardième de mètre, la goutte qui l'a matérialisé quelque part est un milliard de fois plus grosse. Dire que cette trace visible à l'œil nu est la trajectoire de la particule a aussi peu de sens que de dire, pour un bouchon de liège dérivant sur la Seine, que la trajectoire du bouchon, c'est le lit de la Seine (qui pourtant ne fait pas un milliard de centimètres de large)...
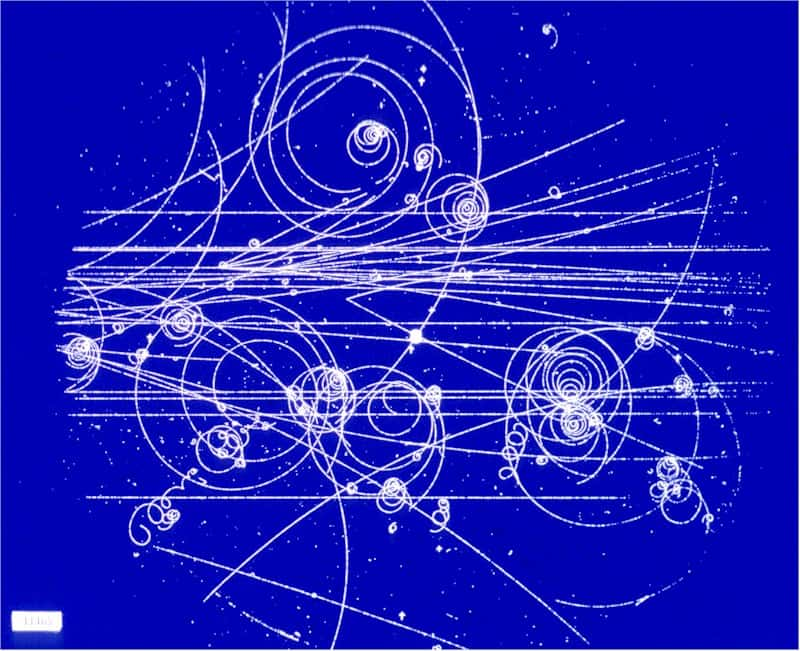
Une image prise dans une chambre à bulles, héritière de la chambre de Wilson, montrant les trajectoires des particules courbées par un champ magnétique sous forme de minuscules bulles engendrées par leur passage. Le sens de la courbure donne le signe de la charge de la particule, et le rayon de courbure mesure la quantité de mouvement. © Cern
Pas de trajectoire, et pourtant elle existe pour une bille lancée en l'air. Alors, comment passe-t-on de la situation quantique à la situation « normale » (classique) ? Schématiquement, quand la particule quantique, grossissant au moins par la pensée (la nôtre), cesse-t-elle d'être ce fantôme erratique présent partout et nulle part pour gentiment se replacer, instant après instant, sur une ligne continue se développant dans l'espace ? Cette question n'a pas encore de réponse complète et détaillée, mais Feynman a forgé la clé pour ouvrir sans la forcer la porteporte à la compréhension de cette transition mystérieuse et indiscutable, grâce au formalisme qu'il a inventé, jetant ainsi sur les fondements quantiques une lumière transparente.

Richard Feynman était un physicien de génie et un enseignant hors pair. En reformulant la théorie quantique à l'aide de son intégrale de chemin, il a révolutionné la théorie quantique des champs et des particules élémentaires. On lui doit des réflexions visionnaires sur la nanotechnologie et les ordinateurs quantiques. © American Institute of Physics
Ce formalisme est trop technique pour pouvoir être seulement résumé, mais il est possible de s'en faire une idée par une image qui n'est pas sans risques. Il faut se représenter l'évolution spatiale d'un petit objet non comme le parcours le long d'une ligne, mais comme un voyage explorant tout l'intérieur d'un tube d'espace-temps où l'on peut trouver cette particule : la dimension transversale du tuyau évoque le flou de la position, et comme on ne saurait privilégier un point puisqu'il y a dans le tube autant de lignes que l'on veut, pas question de fixer aussi une tangente (tangente à quoi d'ailleurs ?). Ce tube contient une infinité de chemins reliant une de ses extrémités à l'autre et, si l'on y tient vraiment, on peut dire que la particule emprunte toutes ces « trajectoires » à la fois, toutes participant à l'évolution d'un endroit à l'autre entre deux instants. Pas simple, mais c'est ainsi. Pire encore qu'une trajectoire brownienne où, s'il n'y a toujours pas de vitesse (la trajectoire n'est nulle part dérivable), au moins, il y a une position, on n'a pas tout perdu.
Que se passe-t-il quand l'objet est de plus en plus gros et se métamorphosemétamorphose peu à peu en une petite bille que l'on peut tenir au creux de la main ? Simple : la dimension transversale du tube diminue sans cesse et, quand on passe à la limite classique, devient une ligne -- ça, c'est évident --, mais le miracle, c'est que cette ligne, obtenue par passage à la limite à l'intérieur du formalisme quantique, n'est rien d'autre que la trajectoire prévue par GaliléeGalilée, NewtonNewton, Lagrange et Hamilton ! Merci, M. Feynman.