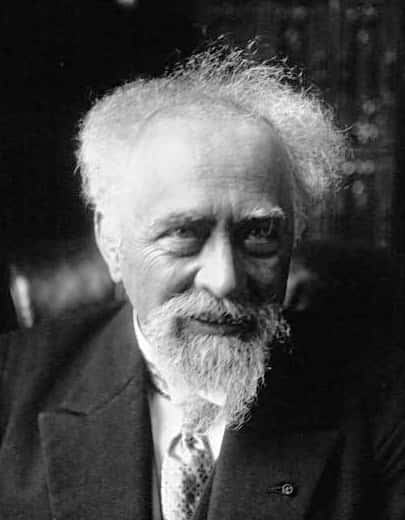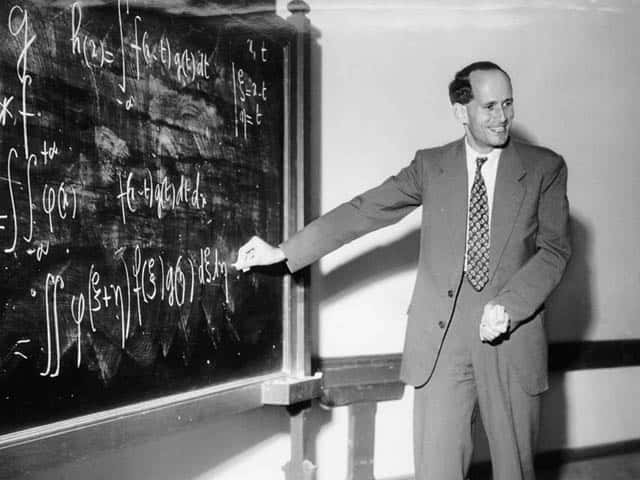au sommaire
Le chaos, au sens banal du terme, est un terme à la mode, trop souvent mis à toutes les sauces. Pour les scientifiques, il s'agit d'un nouvel ordre, insoupçonné pendant des siècles de déterminisme triomphant, dont le champion à l'époque moderne fut le grand Laplace.
Au début du XXe siècle, Poincaré ne fit pas que lever un coin du voile sur un univers inconnu, mais ses travaux précurseurs et visionnaires restèrent presque sans suite jusqu'au début des années 1960.
À ce moment précis, un déclic se produisit, sorte d'impetus, pichenette décisive pour mettre en mouvement ce qui ne l'était pas. Pour cela, il fallut un météorologuemétéorologue inspiré, Edward Lorenz, et un ordinateurordinateur qu'avec nos yeuxyeux d'aujourd'hui, l'on prendrait plutôt pour un char à bœufs. Les anecdotes fleurissent autour de la découverte de Lorenz, mais ce qui est important est ce qui s'est ensuivi : l'essor prodigieux d'une discipline en conséquence de ce que certains considèrent à tort ou à raison comme un accidentaccident heureux de l'histoire des sciences.
Devenu presque une discipline en soi, le chaos appartient au domaine des phénomènes dits non linéaires, ceux qui sont caractérisés par le fait que, très schématiquement parlant, si vous agissez deux fois plus sur un système, celui-ci ne réagit pas deux fois plus : l'effet n'est pas proportionnel à la cause. Un exemple : posez délicatement une petite bille sur une orange. Rien ne se passe, jusqu'au moment où un petit rien lui fait perdre l'équilibre et la fait chuter. Autrement dit : petites causes, grands effets, ou encore « effet papillon ». Notez que l'inverse est d'ailleurs aussi possible : on agit beaucoup et rien n'arrive, le frottement solide en est la preuve quotidienne.

Mathématicien, physicien et philosophe de génie, Henri Poincaré (1854-1912) avait anticipé la théorie du chaos. © Laboratoire d'histoire des sciences et de philosophie, archives Henri Poincaré, CNRS, université de Lorraine
Discipline en soi, ce que l'on appelle désormais la théorie des systèmes dynamiques est un nouvel exemple de convergence entre mathématiques et bien d'autres spécialités, la physique bien sûr, mais aussi l'astronomie, la géophysique, l'économie, l'étude des comportements sociaux ou animaux (qui se ressemblent souvent) ; la liste est inépuisable. Elle est une source d'émerveillement et de fascination tant les modélisations les plus simples, dont les équationséquations de départ pourraient figurer dans les livres de collège, donnent lieu aux manifestations les plus ahurissantes. La plus célèbre d'entre elles est l'applicationapplication dite logistique, dont personne ne sait au juste pourquoi Pierre-François Verhulst, dans ses travaux autour de 1840 sur la croissance des populations, a décidé de l'appeler ainsi, sans imaginer que plus d'un siècle plus tard elle deviendrait le bréviaire d'une armée de scientifiques n'en croyant pas toujours leurs yeux devant les richesses fabuleuses qu'une minable fonction du second degré peut engendrer. On doit à Feigenbaum, trentenaire fantasque passé par le MIT, la compréhension en profondeur de phénomènes stupéfiants rassemblés dans une expression mathématique presque triviale, dont il faut souhaiter qu'elle ne disparaisse pas des programmes dispensés à tous, y compris à ceux qui ne rêvent nullement chaque nuit de devenir mathématicienmathématicien ou physicienphysicien.
Ouvrir un livre sur cette question, c'est partir dans un voyage qui vous emporte aux confins de l'imagination la plus débridée. Impossible d'en décrire les mille recoins, les mille facettes, mais il faut vouloir se laisser perdre dans les profondeurs des attracteurs étranges, découvrir les conséquences de la sensibilité aux conditions initiales -- conséquences à la fois factuelles et méthodologiques --, ne pas se bercer d'illusions devant un grand calme spatio-temporel qui, parfois longtemps après, très longtemps après, sombre dans la tempêtetempête des intermittences. Ouvrir un tel livre : voici ce que je conseille à qui veut en savoir plus sur ce qui gouverne presque tous les phénomènes naturels, des tremblements de terre aux prévisions météorologiquesprévisions météorologiques en passant par l'instabilité du Système solaireSystème solaire, la Grande Tache rougeGrande Tache rouge de JupiterJupiter et, peut-être, les krachs boursiers.
Si Laplace revenait parmi nous, lui non plus n'en croirait pas ses yeux.

Mitchell Jay Feigenbaum (1944) est un physicien théoricien américain. Il fut l’un des pionniers de la théorie du chaos dans les années 1970. © Predrag Cvitanović, Wikipédia, cc by sa 2.0
Et, une fois encore, cette discipline peut remettre face à face mathématiciens et physiciens, les uns attachés à la notion d'infiniment petit (au sens strict où ils le définissent), les autres imprégnés de l'idée que l'on peut certes couper en morceaux de plus en plus petits le temps, l'espace, la matièrematière, mais que vient un moment où Dame Nature dit « stop », on ne va pas plus loin. Vieille question, sinon querelle, que l'on résume dans l'alternative : discret ou continu ? Nombres entiers ou nombres réels (pour faire simple) ?
En effet, il se trouve -- mais on pourrait multiplier les exemples à l'infini -- que le chaos et toutes les extravagances qui sont les conséquences obligées de l'application logistique ne peuvent survenir que si le temps y est traité d'une façon discrète (une étape, on s'arrête, on repart et ainsi de suite, la notion de quantum indivisible n'étant pas l'exclusivité de PlanckPlanck, mais, là, c'est le temps et non l'énergieénergie qui est quantifié). Si par mégarde, ou pour de très bonnes raisons, on en considère la version cousine où le temps varie de façon continue (l'approche suivie par Verhulst), tout redevient d'une triste banalité : avoir « continuisé » le temps évacue irrémédiablement tout, absolument tout, de ce qui fait la gloire de Feigenbaum -- sans toutefois rien retirer à Verhulst.
Mais alors ? Pour un phénomène qui semble relever d'un scénario modélisable à la Verhulst-Feigenbaum, qu'en est-il ? Il peut devenir chaotique ou non ? On aimerait bien le savoir, en pratique. Une fois encore, la réponse ne saurait être dogmatique, mais pragmatique : tout dépend du contexte. Si l'on analyse un système dont l'échelle de temps propretemps propre est gigantesque par rapport au plus petit intervalle de temps humainement concevable (le temps de Planck, histoire de fixer les idées et d'être sûr de soi), rien ne s'oppose (jusqu'à preuve avérée du contraire) à affirmer que, pour ce système, le temps s'écoule continûment, sans à-coups et sans nécessiter d'introduire ce qu'est la constante de Planckconstante de Planck pour la LuneLune en rotation autour de la Terre. Si à l'inverse seule une stroboscopie temporelle a un sens, ou est susceptible d'être modélisée, alors la variable représentant le temps doit être prise comme les valeurs d'une suite discrète, une succession d'instants bien séparés les uns des autres. Et là, en effet, le chaos guette, mais ce n'est parfois qu'à très grande échelle qu'il peut se manifester (les régimes d'intermittence sont là pour en témoigner). Autrement dit, sur une courte période temporelle, un système peut sembler parfaitement stable et ordonné, pour tout dire imperturbable, mais rien ne permet d'affirmer qu'il en ira ainsi jusqu'à la fin des temps.
Le diable est dans les détails.