Quadrature du cercle : pourquoi dit-on que c'est impossible ?

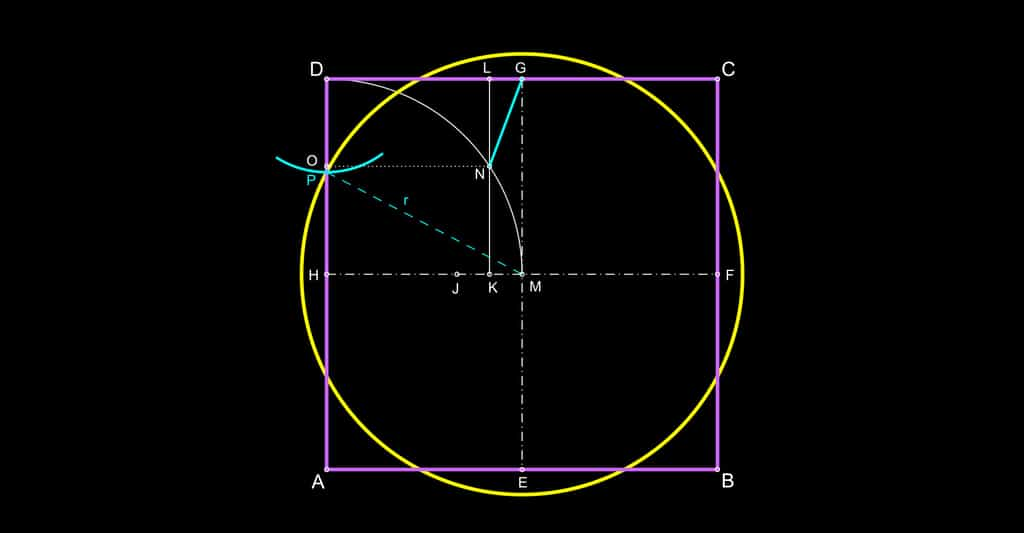
La quadrature du cercle consiste à trouver un carré de même aire qu'un cercle donné, comme le montre le dessin suivant.

À priori, ce n'est pas sorcier, mais les Grecs anciens ajoutaient une condition : il fallait construire le carré à la règle et au compas. Les mathématiciensmathématiciens ont cherché 2.000 ans avant de réaliser que c'était impossible.

Dès l'Antiquité, les mathématiciens ont trouvé des méthodes échappant à cette règle. En voici une qui semble dater du XIX^e siècle.

 

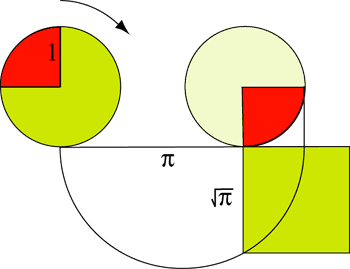
Dans celle-ci, le cercle initial de rayon une unité (à gauche) roule sur une droite, créant une longueur égale à sa demi-circonférence, soit à Π, et une autre égale à Π + 1. Le théorème de Pythagore permet alors de construire la longueur égale à la racine carrée de Π qui est le côté d'un carré de même aire que le cercle initial.

En respectant les règles imposées, la quadrature du cercle a très vite acquis la réputation de problème insoluble si bien que, en 1775, l'Académie des Sciences décida de ne plus recevoir de quadratures.

L’algèbre au secours de la géométrie

Il restait à démontrer que c'était effectivement impossible. La solution à ce problème géométrique vint de l'algèbre en considérant les nombres constructibles à la règle et au compas plutôt que les points, c'est-à-dire les distances entre les points constructibles. Pierre-Laurent Wantzel (1814 - 1848) montra que ces nombres sont racines d'équations algébriques à coefficients entiers. Ferdinand von LindemannFerdinand von Lindemann (1852 - 1939) conclut en montrant que Π n'était pas algébrique (c'est-à-dire transcendant) ce qui mit un terme à la quête de la quadrature du cercle.