au sommaire
Le phénomène de l'intrication quantique est troublant mais il est bien réel comme l'ont montré en 1982 Alain Aspect et ses collègues. Il s'agissait initialement de tester la validité de l'interprétation dite orthodoxe de la mécanique quantique mais de nos jours, l'intrication est intensément étudiée à cause des ses implications pour la cryptographiecryptographie, la téléportation et l'information quantique. En général, les expériences faites pour tester le phénomène de l'intrication quantique reposent sur la mesure de la polarisation de paires de photons jumeaux, ou sur le spin de paires d'électrons jumeaux. Mais en 1935, lorsqu'EinsteinEinstein, Podolsky et Rosen (EPR) ont publié leur célèbre article pour tenter de démontrer que la théorie quantique devait être incomplète, il en était tout autrement.
Pour comprendre l'expérience de pensée proposée par ces trois chercheurs, il faut savoir qu'en mécanique quantique, deux grandeurs physiquesphysiques, comme la quantité de mouvementsquantité de mouvements et la position d'une particule, sont décrites par un objet mathématique appelé opérateur. Il s'agit de grandeurs mathématiques qui obéissent à une algèbre inhabituelle pour des nombres ordinaires, leur produit ne commute pas toujours. On peut se les représenter sous forme d'une matrice, un tableau de nombres.
Un défi aux inégalités de Heisenberg position-impulsion
Cette non commutativité impose alors que lorsque l'on considère un objet avec des grandeurs physiques associées sous forme d'opérateurs, il n'est pas possible de mesurer simultanément ces grandeurs. Pire, la théorie dénie même l'existence simultanée de ces deux grandeurs.
Ainsi, avec un quanta de matièrematière ou de lumièrelumière, on ne peut non seulement pas connaître la position et la quantité de mouvements de cette particule avec une précisions infinie, mais la position et la quantité de mouvements ne sont pas des caractéristiques possédées simultanément par la particule. Cet interdit est bien exprimé par les fameuses inégalités de Heisenberginégalités de Heisenberg.
Ce comportement étrange indique en réalité que dans le monde quantique il n'existe pas vraiment de particule au sens classique du terme, qui pourrait ressembler à une boule de billard. Il existe un objet, un quanta de matière ou de lumière, qui, selon la situation expérimentale, peut être décrit en partie avec des images de position et de quantité de mouvements mais sous réserve que ces images n'existent pas simultanément.
Pour des gens comme Einstein et Schrödinger, une telle situation ne reflétait qu'une impuissance momentanée de la théorie quantique à fournir une image claire et précise de ce qu'il fallait entendre par un quanta de lumière ou de matière dans l'espace et le temps. C'est pour le prouver qu'Einstein, Podolski et Rosen proposèrent un moyen de violer les inégalités de Heisenberg.
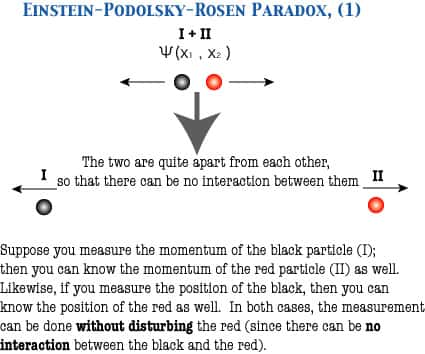
Une particule décrite par une seule fonction d'onde psi (x1, x2) se désintègre par exemple en deux électrons (en noir et en rouge sur ce schéma). À priori, des mesures sur l'un, lorsqu'une grande distance les sépare, ne peuvent influer sur l'état de l'autre. La mécanique quantique réfute cette conclusion. © Soshichi Uchii
Pour cela, ils ont considéré une particule au repos décrite par une fonction d'onde psi, la fameuse fonction donnant l'amplitude de probabilité de trouver un système physique dans un état donné, par exemple de position, d'énergieénergie, de spin, etc.
La particule se désintègre en donnant deux autres particules, par exemple un électron et un positronpositron se déplaçant presque à la vitesse de la lumièrevitesse de la lumière. La conservation de la quantité de mouvements fait que positron et électron partiront dans des directions opposées et avec des quantités de mouvements identiques en valeur absolue.
Mesurons précisément la quantité de mouvements d'une des particules (par l'exemple la noire sur les deux schémas). On connaît à priori instantanément la valeur de l'autre (rouge). Réalisons simultanément une mesure de la position sur la deuxième particule. On devrait pouvoir aussi connaître sa position avec la précision désirée.
Il semble donc que l'on ait violé les inégalités de Heisenberg, à moins d'imaginer un signal envoyé par le premier électron vers l'autre pour brouiller toute mesure de sa position. Mais si l'on considère la mesure de la quantité de mouvements du premier électron six mois après son émissionémission, pour respecter la théorie quantique, il faut que le signal rejoigne instantanément le second électron à une année-lumièreannée-lumière de là. On obtient donc une contradiction avec la relativité restreinte, indiquant un problème dans la théorie quantique et donc la nécessité de la modifier.

Les deux électrons ne peuvent pas être considérés comme deux systèmes séparés décrits par deux fonctions d'onde de la forme psi(x1) psi(x2), il y a intrication, et l'on ne peut violer les inégalités de Heisenberg. On pourrait penser mesurer l'impulsion p de la particule I et la position q de la particule II avec une précision illimitée. On en déduirait la position et l'impulsion de la particule II là aussi avec une précision illimitée mais la mécanique quantique, via l'intrication, l'interdit. © Soshichi Uchii
C'est du moins ce que Einstein pensait mais Niels BohrNiels Bohr n'a pas tardé à contrer cet argument en répliquant qu'il n'était pas possible de parler de phénomènes physiques ni d'objets possédant telle ou telle propriété, indépendamment de la situation expérimentale dans le formalisme de la théorie quantique.
Ainsi, dans l'exemple précédent, électron et positron sont en fait intriqués et ne sont pas décrits par deux fonctions d'ondes indépendantes avant toute mesure. Il n'existe qu'une seule fonction globale, un seul objet, et on ne peut pas parler de deux objets séparés dans l'espace et dans le temps.
L'ensemble réagit d'un bloc lors d'une mesure, quelles que soient les distances, et exhibe une non localité. Cette dernière propriété est malgré tout en accord avec la relativité restreinterelativité restreinte car le flou quantique interdit de pouvoir prédire le résultat des deux mesures. On ne peut pas s'en servir pour transmettre de l'information.
Une source pratique d'atomes jumeaux
Dans un article publié dans Nature, un groupe de trois chercheurs (allemand, autrichien et français) vient de montrer qu'il était possible d'obtenir des particules qui devraient être intriquées et qui ne seraient pas des photons ou des paires électron-positron mais des objets plus gros, des atomesatomes !
On devrait pouvoir réaliser sur eux des mesures de position et d'impulsion, comme l'avaient proposé par Einstein, Podolski et Rosen en 1935. On peut aussi imaginer des expériences faisant intervenir des états de spins de ces atomes, comme pour les paires des photons jumeaux. De fait, l'expérience réalisée par les chercheurs de la Technischen Universität (TU) Wien (l'Université de Technologie de Vienne) est l'analogue avec les ondes de matière de la génération non-linéaire de paires de photons intriqués bien connue dans les expériences modernes sur l'intrication.
Selon les propres mots des chercheurs, ils ont obtenu des faisceaux d'atomes jumeaux à partir de quasi-condensats de Bose-Einstein (CBE). Plus précisément, ils sont partis d'un gazgaz d'atomes de rubidiumrubidium neutres qu'ils ont piégé et refroidi en dessous du millionième de kelvinkelvin, jusqu'à obtenir une condensationcondensation de Bose sur un dispositif similaire à une puce électronique.
Cette « puce atomique » permet de manipuler les atomes du condensat de BE avec une très grande précision. En particulier, on peut transférer des quanta d'énergie vibrationnelle un à un au CBE. On peut donc exciter les niveaux d'énergie du CBE de telle sorte qu'il se retrouve juste au-dessus de son état fondamentalétat fondamental. Les calculs montrent alors qu'il n'a pas d'autre choix que de se désexciter en émettant justement deux atomes corrélés avec des impulsions opposées. Ces atomes devraient bel et bien former un seul système quantique et on devrait pouvoir démontrer expérimentalement qu'un effet EPR se manifeste si l'on cherche à mesurer simultanément la position et l'impulsion de l'un d'entre eux, ou deux valeurs de spin portés par la structure hyperfine des électrons des deux atomes formant un état intriqué par exemple.
Reste à voir ce que ces expériences vont donner une fois qu'on les aura réalisées...