au sommaire
Il est impossible de dresser la table précise des records du « plus grand nombre premier connu » avant le XVIe siècle : peu de documents des siècles précédents nous sont parvenus.

Il est inconcevable de valider une affirmation de primalité quand elle n'est pas accompagnée d'un minimum de justifications. C'était rarement le cas avant le mathématicienmathématicien de la Renaissance Pietro Cataldi, et même quand ce dernier commente ses découvertes, on a du mal à savoir quels calculs il a réellement effectués.
Afin de comprendre la nécessité de telles justifications, imaginons qu'il suffise à un mathématicien d'affirmer que tel nombre est premier pour qu'on considère (une fois la primalité démontrée) que ledit mathématicien détenait le record du plus grand nombre premier. Celui qui affirme que tous les nombres de Mersenne (Mp = 2p - 1, avec p premier) sont premiers détiendrait alors le record jusqu'à la fin des temps : en effet, une infinité de ces nombres sont vraisemblablement premiers ; par conséquent, même si notre mathématicien se trompe pour certains, il sera toujours celui qui a énoncé un nombre premier plus grand que tous ceux qui sont connus à un instant donné.

Histoire du plus grand nombre premier
L'histoire du plus grand nombre premier commence donc à la fin du XVIe siècle : en 1588, Pietro Cataldi vérifie que les nombres de Mersenne M17 = 217 - 1 = 131.071 et M19 = 219 - 1 = 524.287 sont premiers. La table de nombres premiers qu'il a établie jusqu'à l'entier 750 (dont le carré est 562.500) est l'indice qu'il a bien effectué les calculs nécessaires pour prouver la primalité de ces deux nombres. Malheureusement, Cataldi indique aussi que Mn = 2n - 1 est premier pour n = 23, 29, 31 et 37 ; or c'est faux, sauf pour n = 31.
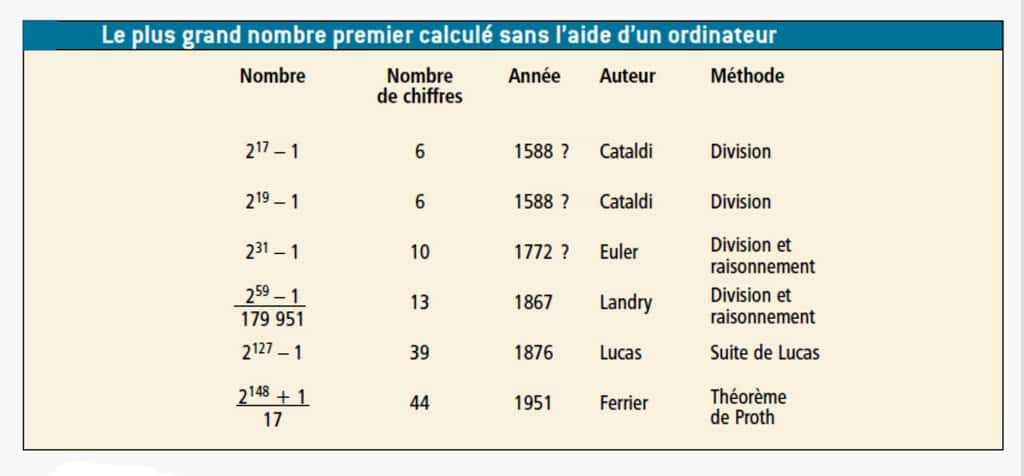
En 1640, Fermat, qui avait découvert que « si p est impair et premier, alors les diviseurs premiers de 2p - 1 sont de la forme 2ap + 1», utilise ce résultat pour montrer la fausseté des affirmations de Cataldi sur la primalité de M23 et de M37. Plus tard, Euler montre que Cataldi avait raison pour M31 et se trompait pour M29. Assez étrangement, les facteurs trouvés pour M23, M29 et M37 sont assez petits : si Cataldi avait utilisé sa table systématiquement, il aurait dû les découvrir. Cela, bien sûr, jette un doute sur le sérieux de ses affirmations pour M17 et M19.

Après Fermat et Euler, et à l'image de leurs propres contributions, l'histoire du plus grand nombre premier est celle des progrès dans les méthodes, plutôt que celle de l'obstination de calculateurs prêts à effectuer des suites d'opérations de plus en plus longues et pénibles pour un record. Bien sûr, quand on dispose d'un ordinateur puissant en plus d'un crayon et du papier, on envisage plus aisément de faire quelques calculs. Toutefois, les derniers records, obtenus en faisant calculer de très nombreuses machines en réseau, ne contredisent pas le principe précédent : le record du plus grand nombre premier reste le fruit de l'intelligenceintelligence et de l'innovation. La nouveauté présente dans les derniers calculs n'est pas strictement mathématique, mais réside dans la maîtrise et l'application, parfaitement optimisée et organisée à grande échelle, d'une technique nouvelle. En ce domaine, pas plus qu'en mathématiques, on ne réussit par le seul acharnement.
En définitive, le premier record indubitable est la démonstration par Euler que Cataldi avait raison pour la primalité de M31 : entre les années 1753 et 1772 (il est impossible de savoir précisément quand), Euler prouve, par le raisonnement et le calcul, que le nombre de Mersenne 231 - 1 = 2.147.483.647 est premier. Il établit d'abord que les diviseurs premiers de 231 - 1 sont nécessairement de la forme 248n + 1 ou 248n + 63 ; dans un second temps, Euler exploite ce résultat en opérant une série judicieuse et limitée de divisions.

Le record de Landry
Le record suivant est obtenu un siècle plus tard : F. Landry prouve en 1867 que (259 - 1)/179.951 = 3.203.431.780.337 est premier. Ce record doit être remarqué, car le nombre premier trouvé par Landry n'est pas un nombre de Mersenne. De tous les nombres record qui ne sont pas des nombres de Mersenne, c'est celui qui a tenu le plus longtemps : neuf ans.

En 1876, Lucas propose une méthode plus efficace encore que celles de Fermat et d'Euler pour tester si un nombre de Mersenne est premier. Cette méthode est simplifiée par D. H. Lehmer dans les années 1930 et est encore utilisée aujourd'hui pour les records de plus grands nombres premiers ; on l'associe désormais à des techniques de calcul élaborées pour la manipulation des grands entiers, telles que la multiplication par transformée de Fourrier discrète, qui est une innovation des années 1970.

En appliquant sa méthode, Lucas trouve en 1876 le nombre premier de Mersenne suivant :
M127 = 2127 - 1 = 170.141.183.460.469.231.731.687.303.715.884.105.727

Ce nombre de 39 chiffres reste le plus grand nombre premier connu jusqu'en 1951. À cette date, A. Ferrier, en utilisant une réciproque partielle du petit théorème de Fermat et en s'aidant d'une machine à calculer mécanique de bureau, découvre un nombre premier de 44 chiffres et bat ainsi le record de Lucas :

Commence alors le temps des machines électroniques. Depuis leur apparition dans les années 1940, les records de calcul se succèdent au rythme des progrès techniques (rapiditérapidité, fiabilité et puissance des circuits), mais aussi grâce à des innovations dans les algorithmes mathématiques de manipulation des grands nombres et grâce à une meilleure maîtrise des langages de programmation (conception du jeu d'instructions, compilation des programmes, utilisation des mémoires, organisation des calculs).
Dès 1949, le mathématicien M. Newman a tenté de trouver des nombres de Mersenne premiers en utilisant l'un des premiers ordinateursordinateurs, la machine de Manchester, dotée d'une mémoire de 1.024 chiffres binairesbinaires (128 octetsoctets !). Cette machine fut mise au point en 1948-1949 par l'équipe qui avait conçu Colossus, l'ordinateur grâce auquel les Britanniques étaient parvenus à déchiffrer de nombreux messages secrets allemands pendant la seconde guerre mondiale.
Le grand mathématicien et logicien Alan Turing, qui avait participé au projet Colossus, améliora le programme de Newman, mais cette collaboration n'aboutit pas à la découverte d'un nouveau nombre de Mersenne premier.

Les ordinateurs et la course aux nombres premiers
En 1951, J. C. P. Miller et D. J. Wheeler s'engagent dans la course aux nombres premiers à l'aide de l'ordinateur Edsac (Electronic Delay Storage Automatic Calculator) qui, avec sa mémoire de cinq kilo-octets, est moins puissant que nos calculatrices de poche. Ils prouvent que les nombres de la forme k.M127 + 1 sont premiers pour k = 114, 124, 388, 408, 498, 696, 738, 744, 780, 934 et 978. Ces deux chercheurs découvrent aussi que le nombre suivant, qui s'écrit avec 79 chiffres, est premier : 180 x (M127)2 + 1 = 180 x (2127 - 1)2 + 1
Ce nombre n'a gardé le titre de « plus grand nombre premier connu » que peu de temps. L'année suivante, Raphaël Robinson prouve en effet la primalité de cinq nouveaux nombres de Mersenne avec l'ordinateur Swac (Standards Western Automatic Computer). Chose amusante et extraordinaire, le programme utilisé par Robinson était le premier qu'il ait jamais écrit ; or, il fonctionna dès le premier essai, le 30 janvier 1952, et livra dans la journée deux nouveaux nombres de Mersenne premiers (M521, M607). Trois autres nombres de Mersenne premiers furent découverts le 25 juin (M1279), le 7 octobre (M2203) et le 9 octobre (M2281).

En 1957, Hans Riesel découvre que M3217 est premier à l'aide de l'ordinateur suédois Besk. De son côté, Alexander Hurwitz découvre en 1961 que M4253 et M4423 sont premiers à l'aide d'un IBM 7090. Donald Gillies prouve en 1963 la primalité de M9689, M9941 et M11213 avec un Illiac-2, et Bryant Tuckerman, à l'aide du célèbre IBMIBM 360, trouve en 1971 le nombre premier M19937, qui s'écrit avec 6.002 chiffres.
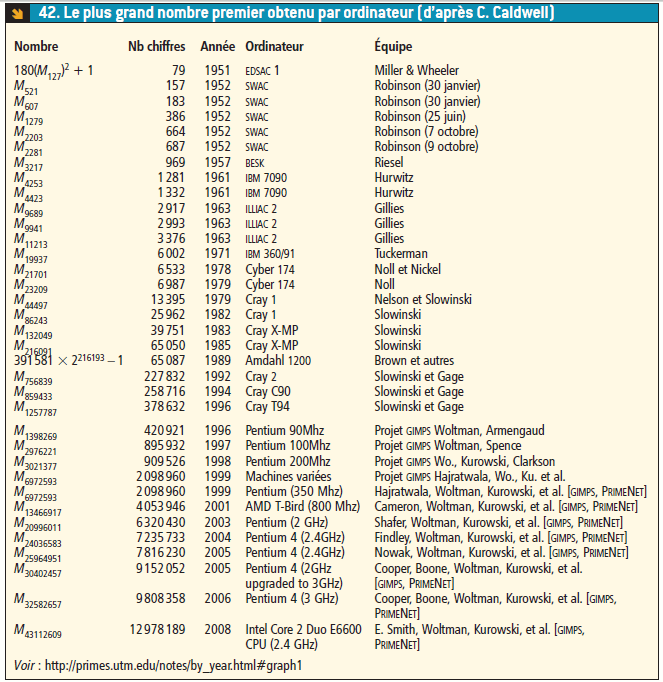
Le calcul de Hurwitz pose un problème étrange et insoluble : à cause de l'ordre dans lequel la machine faisait apparaître les résultats, Hurwitz prit connaissance de la primalité de M4423 quelques secondes avant de lire que le nombre plus petit M4253 est aussi premier. L'ordinateur, quant à lui, avait établi la primalité de M4253 avant celle de M4423. Pour aucun être humain, M4253 n'a donc été un nombre premier record. Seul l'ordinateur IBM 7090 a « vu » que M4253 était premier avant de « voir » que M4423 était premier. Dès lors, doit-on considérer M4253 comme un nombre premier record méritant d'apparaître dans les tables ?