au sommaire
En 1640, le mathématicienmathématicien français Pierre de FermatPierre de Fermat énonçait une conjecture (une affirmation mathématique non démontrée) très importante pour notre propos, car elle est à l'origine de nombreux tests de primalité. Démontrée par le mathématicien suisse Leonard Euler en 1736, elle est désormais connue sous le nom de « petit » théorème de Fermat.

Arithmétique modulaire : le petit théorème de Fermat. © PIRO4D, Pixabay, DP
On ne doit pas confondre le petit théorème de Fermat avec le « grand » théorème de Fermat (démontré en 1995 par le mathématicien britannique Andrew Wiles), lequel indique qu'il n'existe pas de quadruplet de nombres entiers a, b, c, d, avec a, b, c supérieurs à 1 et d supérieur à 2, tels que : ad + bd = cd. Nous présentons le petit théorème de Fermat sous trois formes, chacune possédant son intérêt propre.

Pierre de Fermat a été surnommé « le prince des amateurs » et est l’un des mathématiciens les plus importants du XVIIe siècle. © DP
Petit théorème de Fermat : soit p un nombre premier.
- Forme 1 : pour tout entier a, ap = a (modmod p).
- Forme 2 : pour tout entier a qui n'est pas multiple de p : ap-1 = 1 (mod p)
- Forme 3 : pour tout entier a qui n'est pas multiple de p, il existe un entier k > 0 tel que : ak = 1 (mod p). En outre, le plus petit k > 0 vérifiant cette équation divise (p - 1).
Démontrer le petit théorème de Fermat
Afin de démontrer le petit théorème de Fermat sous ses trois formes, distinguons le cas où a est un multiple du nombre premier p (seule la forme 1 s'applique alors), de celui où il ne l'est pas.
- Si a est un multiple de p, ap l'est aussi, donc ap = a = 0 (mod p) : la forme 1 du petit théorème de Fermat est dans ce cas démontrée.
- Supposons à présent que a ne soit pas un multiple de p. La forme 1 du théorème énonce que ap = a (mod p), égalité qu'il est possible de simplifier par a : le nombre a possède en effet un inverse modulo p, du fait que a et p sont premiers entre eux (puisque p est premier et que a n'est pas multiple de p). L'égalité devient alors ap-1 = 1 (mod p) : c'est l'énoncé de la forme 2 du petit théorème de Fermat, qu'on a ainsi déduit de la forme 1 dans le cas où a n'est pas un multiple de p. Pour prouver le théorème, nous allons démontrer la forme 3, à partir de laquelle nous remonterons aux deux autres formes.
Considérons la suite des valeurs ai, avec i = 1, 2, 3, etc. Aucune de ces puissances de a n'est nulle modulo p : un ai nul signifierait que ai est un multiple de p, c'est-à-dire que p est un facteur premier de ai, donc de a ; or, nous avons supposé que a n'était pas un multiple de p.
Les p nombres a1 (mod p), a2 (mod p), ..., ap (mod p) ne peuvent pas être tous différents, car ils sont tous compris entre 1 et p - 1. Il existe donc au moins deux exposants i et j, 1 ≤ j< i ≤ p, tels que ai = aj (mod p). En multipliant j fois de chaque côté de cette égalité par l'inverse de a modulo p (cet inverse modulo p existe puisque p est premier et que a n'est pas multiple de p, voir précédemment), on obtient ai-j = 1 (mod p). Nous avons donc trouvé un nombre k, compris entre 1 et p - 1, tel que ak = 1 (mod p). Considérons le plus petit nombre k qui vérifie ces conditions. Nous allons montrer que k divise p - 1, ce qui établira la forme 3 du petit théorème de Fermat.
Si ce nombre k divise p - 1, alors il existe un quotient q tel que p - 1 = kq. Pour trouver q et démontrer ainsi le théorème, faisons un détour. Nous allons considérer une relation entre nombres de 1 à p - 1 qui fait intervenir les puissances ai, et qui est définie par l'énoncé suivant : un nombre b est relié à un nombre c s'il existe un exposant i > 0, tel que b = aic (mod p). En utilisant l'existence de l'inverse de a modulo p, on vérifie aisément les propriétés suivantes de cette relation : (I) b est relié à b ; (II) si b est relié à c, alors c est relié à b ; (III) si b est relié à c, et si c est relié à d, alors b est relié à d.
Cette relation est qualifiée de relation d’équivalence, ce qui veut dire concrètement qu'elle range les éléments (les nombres entre 1 et p - 1) en « paquetspaquets » (aussi nommés classes d'équivalence) : les éléments d'un même paquet sont reliés deux à deux, et ceux de deux paquets différents ne sont pas reliés. Montrons que les paquets ainsi définis ont tous le même nombre d'éléments.
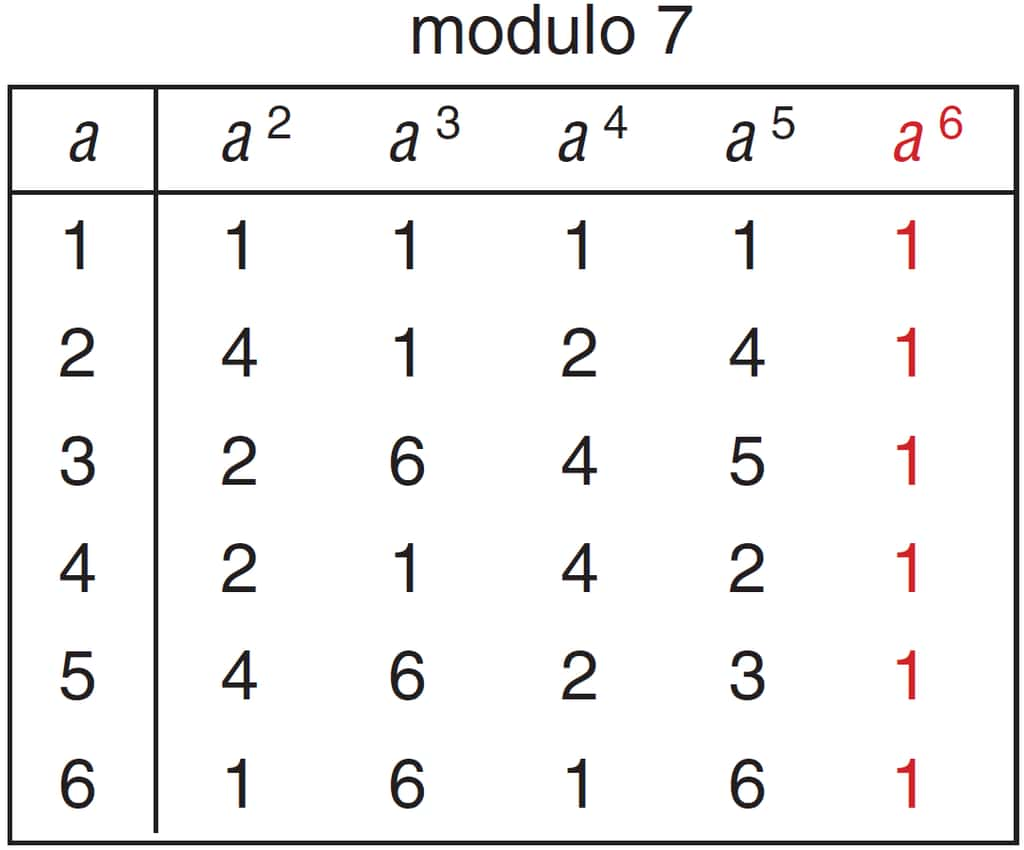
D’après la forme 2 du petit théorème de Fermat, pour un nombre p premier et un nombre a non multiple de p, on a ap–1 = 1 (mod p). On le vérifie ici modulo 7 pour des valeurs de a de 1 à 6 : pour toutes ces valeurs, a6 = 1 (mod 7) (en rouge). © Belin
Soit X un paquet, et b un élément de X. Si c est un autre élément de X, il existe, d'après la définition de la relation, un exposant i tel que c = aib (mod p). En donnant différentes valeurs à l'exposant i, on engendre donc tous les éléments de X.
À ce stade de la démonstration, nous allons retrouver le nombre k défini précédemment. Comme ak = 1 (mod p), il suffit, pour trouver les éléments de X, de considérer tous les exposants i compris dans l'intervalle 0 ≤ i ≤ k - 1. On en déduit que les éléments du paquet X sont exactement les k éléments b, ab, a2b, ..., ak-1b. Il n'y en a pas d'autres, car, pour les exposants supérieurs à k, on retombe sur les mêmes éléments ai : ai+k = ai (mod p). En outre, ces k éléments sont deux à deux distincts : en effet, si deux éléments de rangs i et j dans cette suite étaient identiques, on aurait aib = ajb (mod p) avec 0 ≤ j ≤ i ≤ k - 1, d'où ai = aj (mod p) et ai-j = 1 (mod p) ; comme i - j est inférieur à k, la seule solution est i = j : les deux éléments de rang i et j seraient en fait le même.
Chaque paquet comporte donc exactement k éléments distincts. Soit q le nombre de paquets. Comme le nombre total d'éléments est p - 1 (il s'agit de tous les nombres entre 1 et p - 1), on obtient bien l'égalité recherchée p - 1 = kq.
Nous venons de démontrer la forme 3 du petit théorème de Fermat. On en déduit aisément les formes 1 et 2. À partir de l'égalité p - 1 = kq, avec 1 ≤ q < p - 1, on trouve : ap-1 = akq = (ak)q = 1q = 1 (mod p), d'où ap = a (mod p), ce qui établit les formes 1 et 2 du petit théorème de Fermat.
Les formes 1 et 2 du petit théorème de Fermat peuvent être démontrées plus rapidement de la façon suivante :
Soit a un nombre qui n'est pas un multiple du nombre premier p. L'applicationapplication qui, au nombre n compris entre 0 et p - 1, fait correspondre le produit na (mod p), est une application de l'intervalle 0, 1, ..., p - 1 dans lui-même. Si deux nombres sont différents modulo p (n ≠ m (mod p)), alors leurs images par l'application sont aussi différentes (na ≠ ma (mod p)) : en effet, en multipliant les deux côtés de l'égalité na = ma (mod p) par l'inverse de a (qui existe modulo p, puisque p est premier et que a n'en est pas un multiple), on obtient n = m (mod p). Il en résulte que l'ensemble des éléments a (mod p), 2a (mod p), ..., (p - 1)a (mod p), images des nombres de 1 à p - 1 par l'application, est constitué de p - 1 valeurs différentes. Ces p - 1 valeurs modulo p sont nécessairement comprises dans l'intervalle 1, 2, ..., p - 1. À l'ordre près, cet ensemble est donc exactement l'ensemble 1, 2, ..., p - 1.
Donc : 1.2.3. ... (p - 1) = a.2a.3a. ... (p - 1)a (mod p)
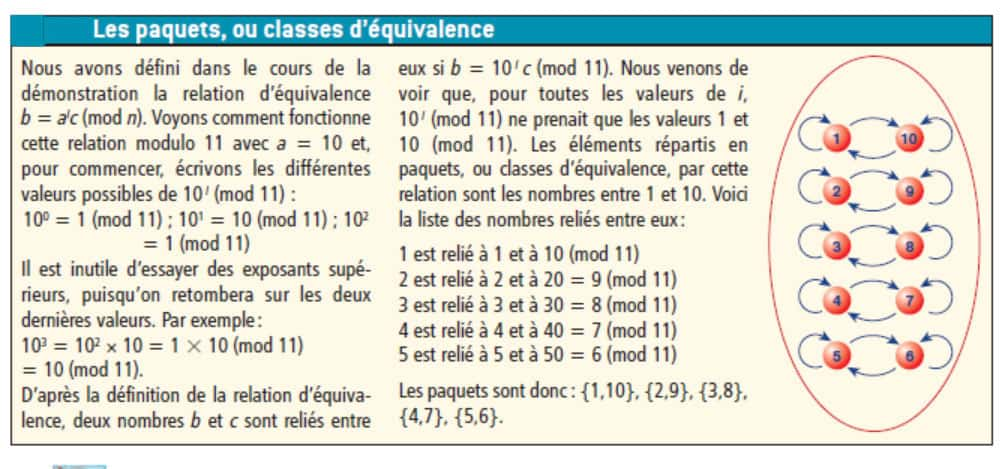
Une explication sur ce que sont les paquets, aussi appelés classes d’équivalence. © Belin
En simplifiant successivement par 2, 3, ..., (p - 1), ce qui est possible, car chaque i, entre 1 et (p - 1), possède un inverse modulo p, on obtient : 1 = ap-1 (mod p).
Cette égalité correspond à la forme 2 du petit théorème de Fermat, à partir de laquelle on déduit aisément la forme 1.























