au sommaire
Un graphe est une collection d'éléments mis en relation entre eux. Géométriquement, on représente ces éléments par des points (les sommets) reliés entre eux par des arcs de courbe (les arêtes). Selon que l'on choisit d'orienter les arêtes ou de leur attribuer un poids (un coût de passage), on parle de graphes orientés ou de graphes pondérés.
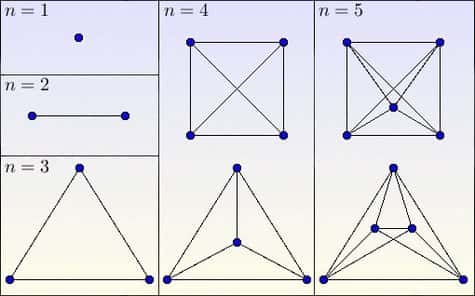
Les graphes complets sont ceux dont tous les sommets sont reliés deux à deux.
Crédits : S. Tummarello
La théorie des graphes s'intéresse à leurs multiples propriétés : existence de chemins les plus courts ou les moins coûteux, de cycles particuliers (eulériens, hamiltonienshamiltoniens, ...)), nombre d'intersections dans le plan, problèmes de coloriage, etc.
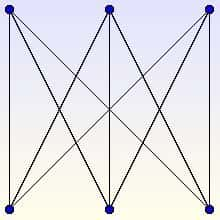
Le graphe K3,3 n'est pas planaire : les arêtes se coupent en au moins un point dans le plan.
Crédits : S. Tummarello
On fait remonter la théorie des graphes au problème des ponts de Königsberg : peut-on organiser dans cette ville une promenade dont le trajet serait une boucle qui passe une fois et une seule par chacun des sept ponts ? En termes modernes, il s'agit de montrer l'existence ou non d'un cycle eulérien dans le graphe associé : Euler a montré en 1736 qu'un tel parcours n'existe pas.
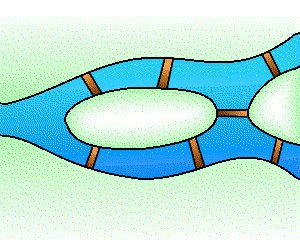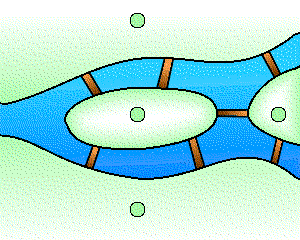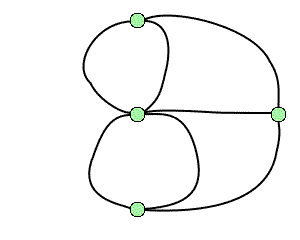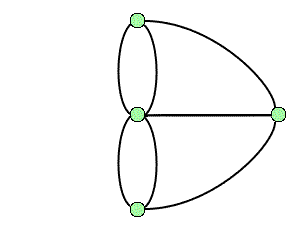
Le graphe associé au problème des ponts de Königsberg.
Crédits : S. Tummarello
Aujourd'hui, les graphes trouvent maintes applications dans la modélisation des réseaux (routiers, informatiques, etc.). Par ailleurs la théorie des graphes a fourni des problèmes en algorithmiquealgorithmique (problème du voyageur de commerce, coloration de graphes, calcul du plus grand sous-graphe commun à deux graphes, etc.), qui sont cruciaux en théorie de la complexité (problèmes NP-complets, conjecture P=NP).























