au sommaire
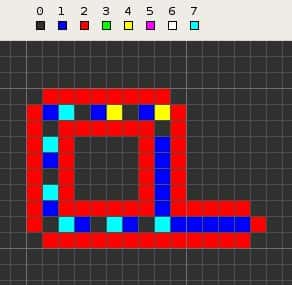
La configuration de départ de la boucle de Langton. Chaque case peut prendre 8 états, codés par un chiffre de 0 à 7 ou, comme ici, par une couleur. Des règles permettent de passer à l'étape suivante, où les cases changeront d'état en fonction de leurs voisines. Avec les règles adoptées, cette structure allonge au fil des étapes l'appendice en bas à droite, lequel se replie pour former une nouvelle structure identique et ainsi de suite. Les cellules à l'état 2 figurent la membrane et les cellules internes contiennent l'information indispensable à la réplication, leur rôle rappelant celui de l'ADN. © Domaine public
La boucle de Langton est une forme autoréplicante dans un certain automate cellulaireautomate cellulaire, inventée en 1984 par le mathématicienmathématicien Christopher LangtonChristopher Langton. Dans ces « jeux de la vie », des règles permettent de faire évoluer étape par étape des cases dessinées sur un quadrillage.
John von NeumannJohn von Neumann, inventeur du concept, a créé un automate capable de se reproduire avec des unités (les cases, ou cellules) pouvant prendre 29 états. Edgar Frank Codd l'a simplifié à 8 états. Christopher Langton a adopté ce principe mais en partant d'une structure définie à l'avance de sorte que les règles conduisent à son autoréplication. En somme, la faculté de se reproduire est codée dans la structure elle-même et sa forme rappelle d'ailleurs celle d'un organisme vivant.
















