Vers une solution pour le problème à trois corps

Isaac NewtonIsaac Newton, on ne le présente plus. Il est notamment à l'origine de la mécanique classique et de la théorie de la gravitation universelle. Ces lois ont jeté les bases de la mécanique céleste. Mais aussi d'une énigme qui a empêché les physiciensphysiciens de dormir pendant plusieurs siècles, celle du problème à trois corps.

Car les lois de Newton permettent d'assez facilement déterminer les mouvements dans le cas simple de deux corps en interaction comme la Terre et le Soleil. Mais les choses se compliquent lorsqu'intervient un troisième corps, la Lune par exemple. Les physiciens ont certes trouvé des solutions pour certains cas particuliers. Mais pas de solution générale.

Aujourd'hui pourtant, une équipe dirigée par des chercheurs de l'université hébraïque de Jérusalem (Israël) pense avoir fait un grand vers la résolutionrésolution de cette vieille énigme. Les physiciens ne prétendent pas détenir la solution exacte et complète au problème à trois corps, cependant ils ont développé une méthode statistique de travail qui pourrait tout de même s'avérer d'une grande utilité.

Comme l’effet papillon, le problème à trois corps est trop chaotique pour qu’on lui applique un modèle mathématique classique. © mycteria, Adobe Stock

S’appuyer sur les statistiques

« Lorsque nous avons comparé nos prévisions à des modèles générés par ordinateursordinateurs des mouvements réels de trois corps célestes, nous avons trouvé un haut degré de précision », explique Nicholas Stone, astrophysicienastrophysicien. Et pour en arriver là, les chercheurs de l'université hébraïque de Jérusalem se sont appuyés sur des travaux antérieurs qui suggèrent que, dans un système à trois corps instable et chaotique, l'un des corps finit toujours par être expulsé. S'établit ensuite une relation binairebinaire entre les deux corps restants : les survivants.

Les chercheurs ont appliqué une hypothèse de probabilité qualifiée d'ergodicité. Une hypothèse qui utilise les principes des moyennes pour déterminer ce qui va se passer dans un système particulier. Pourquoi ? Parce que dans le temps, tout comme les systèmes à trois corps, les processus ergodiques n'ont que peu de rapport avec leur état initial.

Le travail des physiciens de l'université hébraïque de Jérusalem permet donc aujourd'hui de comprendre comment les deux corps restant d'un problème à trois corps chaotiques vont se comporter. Et ce, dans une grande variété de nouveaux scénarios stables. « Prenez trois trous noirs en orbite, explique Nicholas Stone. Leurs orbites deviendront nécessairement instables et même après que l'un d'entre eux aura été expulsé, nous sommes toujours très intéressés par la relation entre les trous noirstrous noirs survivants. »

Le problème à trois corps suggère de nouvelles orbites exotiques

Les spécialistes de mécanique céleste planchent sur le célèbre problème de trois corps s'attirant mutuellement depuis environ 300 ans. Résultat de cette quête : quelques rares familles de solutions particulières. Deux physiciens serbes viennent d'en trouver 13 autres, qui, peut-être, pourraient s'appliquer à des systèmes d'exoplanètesexoplanètes.

Article de Laurent SaccoLaurent Sacco paru le 21/03/2013

On voit sur ces images des familles d'orbites pour un problème à trois corps restreints périodiques et dans le plan, considérées par deux physiciens serbes. Ces orbites sont en relation avec des classes topologiques de lacets sur une sphère avec trois trous (en rouge), au niveau de l'équateur. En bas à droite, on voit la forme réelle d'une famille d'orbites classifiées dans le plan. © Milovan Suvakov, Veljko Dmitrasinovic

Le « problème à trois corps » est un célèbre problème mathématique en mécanique céleste. Il s'agit de trouver toutes les solutions mathématiques possibles des équationséquations différentielles décrivant les mouvements de trois astresastres s'attirant les uns les autres sous l'effet de la gravitation.

Rappelons que Newton fut le premier à trouver puis intégrer, c'est-à-dire résoudre les équations différentielles décrivant les mouvements de deux corps en mécanique céleste. Il lui a fallu pour cela découvrir la loi de la gravitation, le calcul infinitésimal et intégral, et enfin poser les bases de la théorie des équations différentielles. Par la suite, on a rapidement cherché à décrire les mouvements combinés de trois corps bien connus : la Terre, le Soleil et la Lune.

Cette image infrarouge traitée en fausses couleurs montre directement les exoplanètes autour de HR 8799. Il s'agit de planètes géantes, mais il en existe probablement d'autres plus proches de l'étoile centrale et que l'on ne peut pas encore voir. Trouvera-t-on dans un tel système des orbites décrites par l'une des nouvelles solutions au problème à trois corps trouvées par Milovan Suvakov et Veljko Dmitrasinovic ? © NRC-HIA, C. Marois, Keck Observatory

Orbites à trois corps et plus : le Système solaire est-il stable ?

Déjà au XVIII^e siècle, le mathématicienmathématicien Jean d'Alembert et le physicien Alexis Clairaut s'étaient particulièrement penchés sur cette problématique du mouvement des planètes, ce qui les avait conduits à parler de problème à trois corps. Se posa alors avec plus d'intensité la question, déjà perçue par Newton, de la stabilité à long terme des orbites avec trois et même N corps en mécanique céleste. Il n'était pas impossible que les orbites bien régulières du Système solaireSystème solaire ne soient qu'une phase transitoire de celui-ci, quand bien même cette transition pouvait durer des milliards d'années.

Toujours est-il qu'une première famille de solutions particulières exactes a été découverte par Euler et Lagrange à la fin du XVIII^e siècle. Or, pour des cas plus généraux, force était de considérer les équations de mouvement du problème à deux corps, tout en y incluant des termes supplémentaires traduisant l'existence de petites forces perturbatrices. C'est dans ce contexte que se développa la théorie des perturbations en mécanique céleste.

En 1889, le roi Oskar II de Suède, souhaitant fêter son anniversaire, créa sur la proposition du mathématicien Gösta Mittag-Leffler un prix pour récompenser le meilleur mémoire sur le problème à N corps. Le problème fut posé en ces termes, par le grand mathématicien allemand Karl Weierstrass : « Étant donné un système de N corps qui s'attirent mutuellement conformément à la loi de la gravitation, et en supposant qu'il n'y ait jamais de collision entre deux corps, donner les coordonnées des corps individuels, pour n'importe quel moment de l'avenir ou du passé, sous la forme d'une série uniformément convergente dont les termes sont composés de fonctions connues. »

Mathématicien, physicien et philosophe de génie, Henri Poincaré (ici dans son bureau) a révolutionné la mécanique céleste. Il a posé les bases de la théorie du chaos avec les fameux attracteurs étranges, que l'on connaît notamment en météorologie. © Archives Henri Poincaré du Laboratoire d'histoire, des sciences et de philosophie, CNRS, université de Lorraine

Un problème à N corps intégrable

C'est le physicien et mathématicien Henri Poincaré qui remporta ce prix en révolutionnant les méthodes de la mécanique céleste. Ce faisant, il a entrevu la théorie du chaos et a posé les fondements de la théorie moderne des systèmes dynamiques.

Souvent, on affirme que les résultats de Poincaré prouvent qu'il n'est pas possible d'intégrer les équations différentielles du problème à trois corps pour aboutir à une solution générale. La réalité est plus nuancée, et l'on pourrait même dire que cette affirmation est fausse. Comme le mentionne le mathématicien Alain Chenciner de l'Institut de mécanique céleste et de calcul des éphémérides (IMCCE) dans un article de Scholarpedia : « Bien que le problème à deux corps soit complètement intégrable et ses solutions parfaitement comprises, il n'en est pas de même avec les solutions du problème à trois corps, qui peuvent être d'une complexité arbitraire et sont très loin d'être entièrement comprises. »

En fait, ce que Poincaré a démontré, c'est qu'en supposant certaines conditions assez raisonnables pour l'expression analytique de la solution générale du problème à trois corps, celle-ci n'existait pas. De fait, dès le début du XX^e siècle, le mathématicien Karl Frithiof Sundman a effectivement trouvé une solution très générale et, en 1991, un autre mathématicien, Qiudong Wang, a même trouvé une solution générale au problème à N corps. On parle rarement de ces solutions parce qu'elles sont inutilisables en pratique pour faire des calculs. Il faut calculer des sommes qui convergent extrêmement lentement vers la solution (même pour des distances et des temps courts).

De nouvelles familles de solutions périodiques

S'il n'est pas possible de vraiment trouver une solution générale au problème à trois corps calculable en pratique, il est possible de trouver des familles de solutions particulières qui le sont. Après celles d'Euler et Lagrange, les mathématiciens Roger Broucke et Michel Hénon ont trouvé dans les années 1970 leur solution particulière éponyme. En 1993, le physicien Cristopher Moore du Santa Fe Institute en a dévoilé une autre, qui intègre des orbites en forme de huit.

En bas deux familles d'orbites d’un problème à trois corps restreint périodique et dans le plan, considérées par les deux physiciens serbes. En haut, ces orbites sont en relation avec des classes topologiques de lacets, sur une sphère, avec trois trous (en rouge) au niveau de l'équateur. Sur la partie gauche, on reconnaît une version des orbites en forme de huit, déjà découverte avec le problème à trois corps. © Milovan Suvakov, Veljko Dmitrasinovic

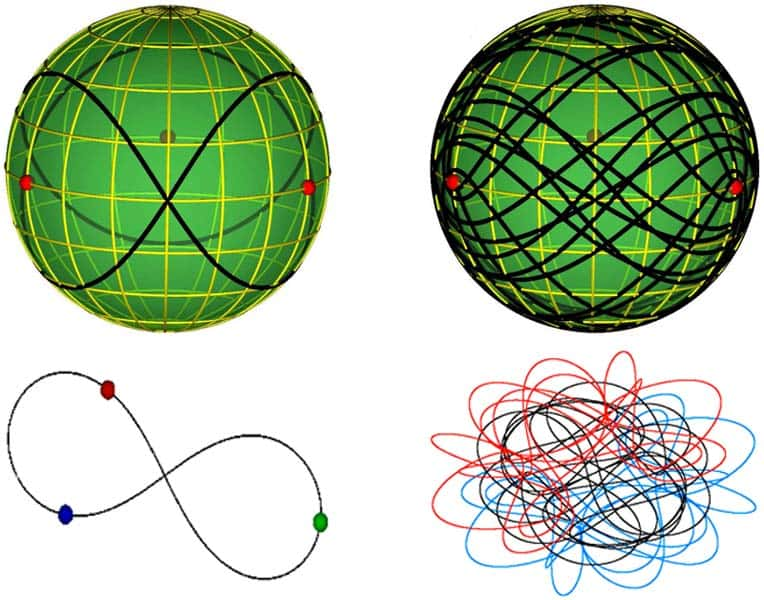
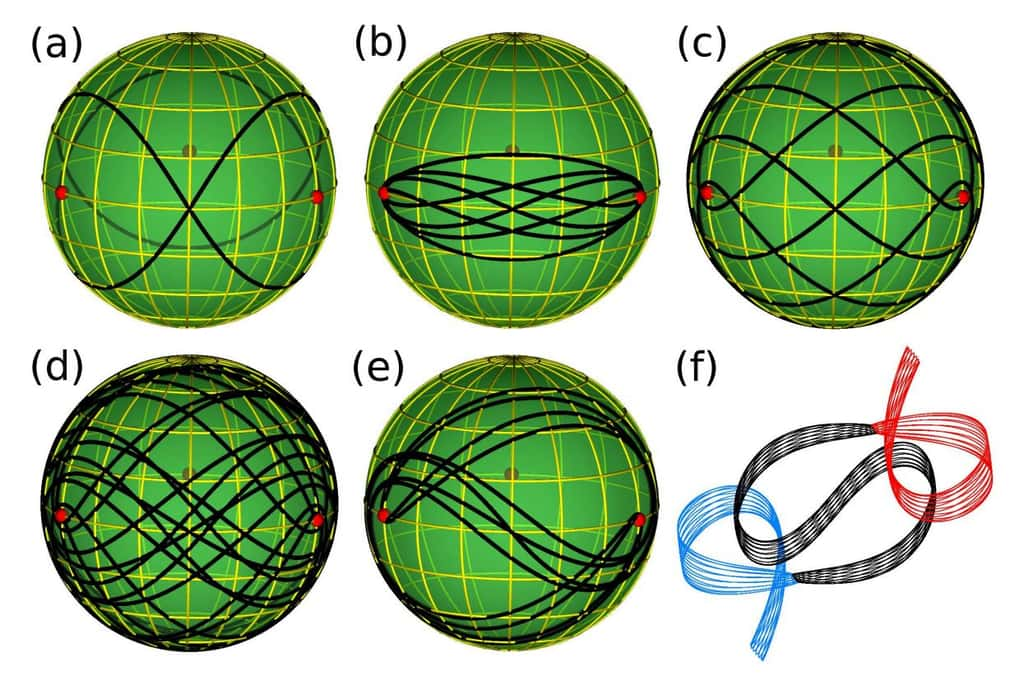
Deux physiciens serbes de l'Institut de physiquephysique de Belgrade, Milovan Suvakov et Veljko Dmitrasinovic, viennent de surprendre en publiant sur arxiv un article dans lequel ils annoncent avoir découvert et classifié 13 nouvelles familles de solutions, à l'aide d'un ordinateur.

Sphère à trois trous et courbes en lacets

Ils ont commencé par considérer un problème à trois corps restreint avec des orbites périodiques dans le plan, des massesmasses égales et un moment cinétiquemoment cinétique total nul. Inspirés par les travaux de Cristopher Moore et Chenciner et Montgomery sur les orbites en forme de huit, ils ont réalisé des simulations numériquessimulations numériques avec différentes conditions initiales.

Les trajectoires complexes des trois corps dans le cas considéré peuvent alors se mettre en correspondance avec des courbes en lacets à la surface d'une sphère avec trois trous. Ces courbes peuvent alors être classées avec des méthodes topologiques et algébriques, ce qui permet du même coup de classifier ces orbites. Selon les physiciens serbes, si ces solutions restent stables quand on les perturbe un peu (en particulier en considérant des masses différentes), il n'est pas impossible qu'elles décrivent ce qui se passe dans certains systèmes d'exoplanètes.