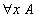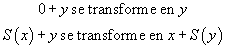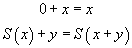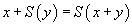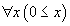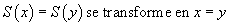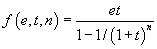
Qu'est-ce qu'une logique ?

Nous avons donc vu comment ajouter un processus de calcul à une logique et les différences que cela induit pour la vérification des démonstrations et la recherche automatique des démonstrations.

Je pense que vous avez deviné la petite pierre que je voudrais apporter à la question « Qu'est-ce qu'une logique? ». La thèse que je voudrais défendre est qu'une logique est composée non seulement de règles de déduction, mais aussi de règles de calcul. Bien entendu, pour chaque logique définie par des règles de déduction et des règles de calcul, on peut construire une logique qui n'a que des règles de déduction et qui démontre les mêmes propositions, l'ensemble des propositions démontrables est le même, mais les démonstrations sont différentes.

Je voudrais, pour terminer, citer deux applications de cette idée. La première reste dans le cadre de l'informatique théorique et la seconde en sort.

Programmer en langage mathématique

La première est la programmation des ordinateursordinateurs en langage mathématique. Si on emprunte une somme e à une banque et qu'on la rembourse en n mensualités et que t est le taux d'intérêt mensuel, le montant des mensualités est donné par la formule

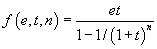
Pour calculer le montant de ces mensualités, l'employé de banque tape sur son ordinateur la somme empruntée, par exemple 30 000 francs, le nombre de mensualités, par exemple 24, et le taux d'intérêt, par exemple 0.0064, et l'ordinateur affiche la somme à rembourser chaque mois. Le programme qui transforme l'information e, t, n en f(e,t,n) n'est, d'un certain point de vue, rien d'autre que la fonction f.
Ce que l'ordinateur affiche est un terme u tel que f(30000,0.0064,24) = u soit une proposition vraie. Mais cette condition n'est pas suffisante : le terme f(30000,0.0064,24) la vérifie car la proposition

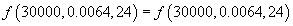
est vraie. Mais si c'est ce terme qui s'affiche sur l'écran de l'ordinateur, cela n'aide pas beaucoup à savoir si on pourra rembourser ces mensualités ou non. On n'attend pas non plus que s'affiche le terme 1300 + 60 - 7, ce qu'on veut c'est le terme 1353. Ce terme est ce qu'on appelle une valeur. L'ordinateur doit donc calculer la valeur associée au terme f(30000,0.0064,24). Identifier programmes et fonctions n'est donc utile que si on formalise les mathématiques dans un système qui comprend des règles de déduction et des règles de calcul, telles que les valeurs soient les formes réduites pour ces règles de calcul.

Pour les fonctions explicitement définissables comme celles-ci, l'arithmétique convient. Mais si on veut utiliser toute la puissance des définitions mathématiques, c'est-à-dire utiliser l'opérateur de descriptions qui permet de définir la fonction prédécesseur sur les nombres relatifs comme la fonction qui à x associe l'unique nombre dont le successeur est x, alors il faut un système de calcul sur ces termes qui est relativement sophistiqué et qui demande en particulier de faire des démonstrations mathématiques des objets à part entière, de manière à ce que l'opérateur de descriptions prenne en argument une démonstration que la définition est correcte, c'est-à-dire que pour tout nombre x il existe un nombre y tel que x soit le successeur de y, et le système de calcul doit, entre autres choses, éliminer les coupures dans ces démonstrations. En effet, si on se contente de la définition « l'unique nombre dont le successeur est égal à x » sans donner de démonstration qu'un tel nombre existe, on ne voit pas par quel miracle on trouverait 4 en appliquant cette expression à 5. En revanche, si on donne aussi une démonstration constructive la proposition « pour tout x, il existe y tel que le successeur de y est égal à x », appliquer cette démonstration au nombre 5 crée une coupure dont l'élimination produit le nombre 4.
La théorie des types de Martin-L (Intuitionnistic type theory, Bibliopolis, Napoli (1984)), Le Calcul des constructionsconstructions (Th. Coquand, G. Huet, The calculus of constructions, Information and Computation 76 (1988) p. 74-85.) et le Calcul des constructions inductives (Ch. Paulin-Mohring, Inductive definitions in the system coq, rules and properties, Typed lambda calculi and applications, Lecture Notes in Computer Science 664, Springer-Verlag (1993) pp. 328-345.) sont des exemples de tels systèmes.

Le sens

La seconde application que je voudrais mentionner est l'impact de cette définition de la notion de logique sur la définition de la notion de sens. Le sens d'une proposition, qu'on oppose à la dénotation, est défini par Frege dans Les lois fondamentales de l'arithmétique : « Nos stipulations déterminent à quelles conditions ce nom de valeur de vérité dénote le vrai. Le sens de ce nom est la pensée que ces conditions sont remplies. » En des termes plus modernes, Michael Dummett définit ainsi le sens : « Nous n'expliquons plus le sens d'un énoncé en stipulant sa valeur de vérité en termes des valeurs de vérité de ses constituants mais en stipulant à quelles conditions on peut l'asserter et ce en termes des conditions auxquelles ses constituants eux-mêmes peuvent être assertés. » (M. Dummett, Philosophie de la logique, Minuit (1991) p. 67).
Autrement dit, le sens d'un énoncé A, est ce qu'il faut faire pour asserter cet énoncé, pour le démontrer. Le sens d'un énoncé de la forme « A et B » est ce qu'il faut faire pour asserter cet énoncé et ce qu'il faut faire c'est asserter A et asserter B. Cela donne la règle de déduction naturelle d'introduction de la conjonction « et ». Cette règle est le sens de la conjonction « et ». Et ce sens, nous ne savons pas l'exprimer autrement qu'en donnant cette règle.

Cette notion de sens permet de définir le sens des connecteurs et des quantificateurs. On peut également définir ainsi le sens des symboles de prédicat et de fonction d'un langage, par exemple, la notion de parallèle est définie par les axiomes de la géométrie. Cette idée rejoint celle de Poincaré selon laquelle les axiomes de la géométrie sont des « définitions déguisées ». On n'a pas d'autre moyen de définir la notion de parallèle qu'en donnant les axiomes de la géométrie. Cela marche bien pour expliquer le sens de petits bouts de phrases : les connecteurs, les quantificateurs, les symboles de prédicat, etc. Mais cela peut-il nous aider à comprendre le sens de phrases complètes ?

Plus simplement cela peut-il nous aider à comprendre à quelle condition deux propositions A et B ont le même sens. Si on parvient à définir cette relation d'équivalence « avoir même sens que », on pourra se contenter de définir le sens d'une proposition comme sa classe d'équivalence pour cette relation. Cela permet d'évacuer le problème de la nature du sens et de le définir, en quelque sorte, à un isomorphisme près. Si on suit cette définition du sens comme « condition d'assertabilité », deux propositions A et B ont le même sens si ce qu'il faut faire pour démontrer A est la même chose que ce qu'il faut faire pour démontrer B. Mais, dans un cadre dans lequel on n'a que des règles de déduction, une démonstration ne peut être à la fois une démonstration de A et une démonstration de B que si A et B sont identiques. Si elles sont différentes, deux propositions ont donc toujours un sens différent, car elles ne peuvent pas partager de démonstration.

Quand on définit une logique avec des règles de déduction et des règles de calcul, on a une équivalence plus faible selon laquelle deux propositions ont le même sens si elles ont la même forme réduite, c'est-à-dire sont égales dans le quotient. Autrement dit, le calcul n'a pas de sens : calculer dans une proposition n'affecte pas le sens de la proposition.

Une première conséquence est que le sens d'une proposition dépend des conventions de calcul choisies. Si on ne prend aucune règle de calcul, les propositions 9 + 57 = 66 et 66 = 66 ont des sens différents. En revanche, si on prend les règles de l'addition comme des règles de calcul, ces deux propositions ont le même sens. Il y a quelque chose d'un peu choquant à ce que le sens d'une proposition dépende de conventions. Mais le même problème se pose avec la dénotation : l'hypothèse du continu ne dénote « vrai » ou « faux » qu'en fonction des axiomes qu'on pose, c'est-à-dire des conventions de raisonnement. De la même manière que la dénotation d'une proposition est déterminé par les conventions de raisonnement, le sens d'une proposition est déterminé par les conventions de calcul.
Une autre conséquence, qui est plus troublante, est que le problème de l'égalité de sens de deux propositions est décidable, puisqu'il suffit de comparer leur formes réduites. Mais pourrions nous dire que deux propositions ont le même sens si en les regardant nous n'étions pas capables de nous en rendre compte ?