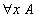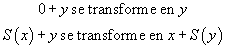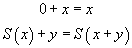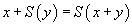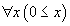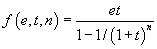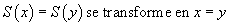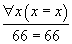
Décidabilité de la relation entre démonstrations et propositions

Étendre ainsi la notion de système formel sur des ensembles de propositions ou sur des propositions réduites pose quelques problèmes. En particulier, il se pose la question de savoir si les démonstrations restent convaincantes. Quand on regarde une démonstration, aussi complexe soit-elle, on doit être capable de vérifier, étape par étape, qu'elle est correcte. Sinon, ce n'est pas une démonstration. La démonstration doit véhiculer toute l'information nécessaire pour que le lecteur puisse lui-même se convaincre que la justesse de ce qui est démontré. Par exemple, si on a la démonstration

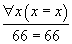
et qu'on prétend que c'est une démonstration de la proposition 9 + 57 = 66, il faut faire un tout petit effort pour se convaincre que la démonstration est correcte. Il faut se convaincre que la conclusion 66 = 66 de cette démonstration et la proposition 9 + 57 = 66 appartiennent bien à la même classe, c'est-à-dire qu'elles ont la même forme réduite. Pour cela, il faut calculer les formes réduites de ces deux propositions. Il y a un peu de travail à faire, mais ce travail peut être fait car le système des règles de calcul a les propriétés de terminaison et de confluence, ce qui permet de réduire les propositions et de vérifier que leurs formes réduites sont identiques. Il n'y a donc pas de perte d'information en passant d'une démonstration en arithmétique à une démonstration dans le quotient. L'information qui semble perdue n'est pas pertinente car il est possible de la reconstituer.

Mais, il y a plus grave : toujours avec cette règle d'élimination du quantificateur universel, on prend un autre axiome

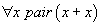
et on donne la démonstration

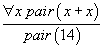
Pour vérifier que cette étape de démonstration est correcte, il faut retrouver le terme par lequel la variable x a été remplacée. Ici, on devine que c'est le terme 7. On peut d'ailleurs se demander, même quand il n'y a pas de règles de calcul si une applicationapplication de la règle d'élimination du quantificateur universel peut toujours être vérifiée. Par exemple, pourquoi est on convaincu que la démonstration

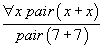
est correcte ? C'est parce qu'il est possible de comparer les propositions

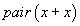
et

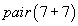
pour trouver que la variable x a été substituée par 7. Cette comparaison a un nom technique, elle s'appelle le filtrage. Le filtrage dans les langages de premier ordre est décidable. Mais, quand on a des règles de calcul, le problème est un peu différent : le problème est de savoir s'il est possible de substituer la variable x dans la proposition

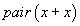
par un terme, non pour obtenir la proposition

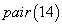
mais une proposition qui a même forme réduite que

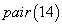
La décidabilité de ce problème dépend beaucoup des règles de calcul considérées. Avec des règles pour l'addition et la multiplication, le filtrage est décidable, si on ajoute la soustraction il devient indécidable.

Quand les règles de calcul sont telles que filtrage est indécidable, il faut changer un peu la grammaire des démonstrations pour qu'on puisse continuer à les vérifier : il faut indiquer le terme substitué dans la règle d'élimination du quantificateur universel pour qu'il n'y ait plus rien à deviner. Alors, pour vérifier une démonstration, il suffit de substituer la variable dans la prémisse de la règle par le terme donné et de vérifier que la proposition obtenue a la même forme réduite que la conclusion.

Si on formule les raisonnements, non en déduction naturelle, mais dans les systèmes à la Frege-Hilbert, le même problème se pose pour savoir si l'ensemble des formes réduites des axiomes logiques

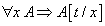
est décidable.