Pourquoi peut-on se parler d’un quai à l’autre du métro ?

La forme des plafonds des stations de métro traditionnelles est celle d'une courbe célèbre, étudiée depuis l'Antiquité, l'ellipse. L'ellipse peut se définir d'une manière la rendant facile à dessiner. C'est la courbe idéale pour former un parterre de fleurs : esthétique et facile à construire. Pour cela, il vous faut trois piquets et une corde. Vous plantez deux piquets et y attachez la corde. Elle doit rester molle. Vous prenez alors l'autre piquet en main et tendez la corde. La courbe décrite par ce piquet mobilemobile (M) quand vous tournez autour des deux piquets fixes (A et B) est une ellipse. Les deux points où sont plantés les piquets sont appelés les foyers de l'ellipse.

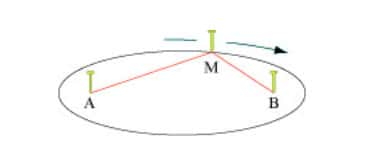
Foyers de l’ellipse : quelles propriétés ?

L'ellipse a une propriété acoustique intéressante faisant intervenir ses deux foyers. Si vous vous placez au niveau de l'un d'eux et parlez, votre voix se réfléchit sur l'autre. Même si, dans un premier temps, il se disperse, le son est ensuite concentré sur l'autre foyer, si bien qu'il est audible de l'autre côté. Cette propriété fut utilisée dans les hôpitaux au Moyen Âge. Les plafonds avaient une forme elliptique, ce qui permettait aux prêtres de confesser les mourants sans risquer la contamination, du moins l'espéraient-ils. Chacun était placé en un foyer de l'ellipse et le son de sa voix était concentré sur l'autre. Le plafond d'une salle de l'abbaye de La Chaise-Dieu (Haute-Loire) a cette forme. On y confessait autrefois les lépreux.

Cette propriété fonctionne dans les stations de métro parisien dont la voûte est en forme d'ellipse. On peut se parler d'un quai à l'autre sans élever la voix et sans être entendu de tous. Il suffit de se placer face à face, un peu devant les chaises, où se tenaient autrefois les poinçonneurs, pour cette raison.

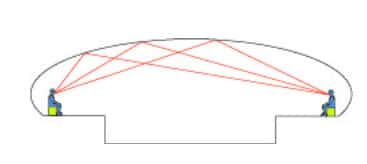
Cette propriété acoustique se retrouve en optique. Si les mursmurs d'une station de métro étaient faits en matière réfléchissante, les rayons lumineux issus d'un foyer se réfléchiraient sur les parois pour se concentrer sur l'autre foyer. De là vient l'expression « se focaliser ». Cette propriété de l'ellipse est appelée sa propriété focalefocale.