Jeu mathématique : quel est l'âge du capitaine ?

« Puisque tu fais de la géométrie et de la trigonométrie, je vais te donner un problème : un navire est en mer. Il est parti de Boston chargé de coton, il jauge 200 tonneaux, il fait voile vers Le Havre ; le grand mât est cassé, il y a un moussemousse sur le gaillard d'avant ; les passagers sont au nombre de douze ; le ventvent souffle N.-E.-E. ; l'horloge marque trois heures un quart d'après-midi ; on est au mois de mai... On demande l'âge du capitaine. » 

Voici une énigme de même stylestyle que l'on peut cependant résoudre :

L’âge des enfants

Pour se débarrasser d'un importun qui vient de l'aborder, une femme le prévient : « Je suis mariée et mère de quatre enfants... ».

L'homme répondit étrangement : « Quels sont le produit et la somme de leurs âges ? »

Interloquée, après un rapide calcul mental, la femme répondit : « 126 et la somme est justement le numéro de la maison en face ! »

L'homme réfléchit un instant avant de répondre : « Je ne trouve pas leurs âges. »

La femme, prise au jeu : « Le plus petit ne parle pas encore. »

L'homme : « Maintenant, je sais. »

Question : quels sont les âges des quatre enfants ?

Réponse 

1, 2, 3 et 21. Il existe onze décompositions de 126 en produit de quatre facteurs a, b, c et d. En voici le tableau avec les sommes S.

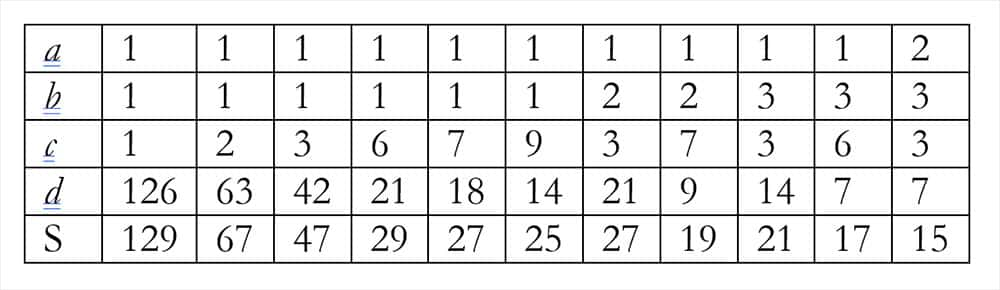
L'homme connaît la somme (le numéro de la maison) mais ne peut conclure. La somme est donc égale à 27, qui correspond à deux décompositions. L'un des cas correspond à deux jumeaux comme « petits derniers », donc la réponse est l'autre.