au sommaire

Page 2
Nous proposons ici un modèle de stockage d'information issu d'une réflexion sur les circuits réverbérants, supports éventuels de la mémoire à court terme. Il ne présente aucune capacité de généralisation, contrairement au modèle de Hopfield mais il se prête à une recherche par le contenu qui le rapproche des mémoires associatives.
1 - mémorisation par superposition de vecteurs transformés sans modulation
1.1- généralités
Le principe de base d'une mémoire associative est que tout élément nouveau est interprété comme un bruit par rapport à l'ensemble des éléments déjà mémorisés par la structure. La réciproque est que les éléments mémorisés forment un bruit pour un vecteur donné.
Dans une mémoire associative de type Hopfield, le vecteur à mémoriser modifie une matrice de valeurs constituée par les éléments déjà mémorisés.
Dans notre modèle, le principe reste le même: le vecteur, après transformation, est superposé aux vecteurs déjà mémorisés et il est considéré comme un bruit par le réseau.
La zone de stockage est représentée par un certain nombre de vecteurs transformés de longueur différente.
Les vecteurs utilisés ont 120 composantes. Chaque composante a pour valeur un niveau de gris 0..100 d'une image 1D.
Exemple:

1.2 phase de stockage
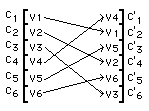
On transforme le vecteur d'origine O de composantes Ci , i 1..n, en un vecteur transformé T de composantes C'i , i 1..d de dimension différente (d) très supérieure à celle du vecteur origine (n).
La formule (1) de calcul de A'1 devient alors:
A'i = i * b modmod (d+1)
où i1..d b premier par rapport à (d+1)
Les composantes C'i d'adresse A'i, i 1..n, ont pour valeurs V'i celles, permutées, du vecteur d'origine.
Les composantes C'i d'adresse A'i, i n+1..d, ont pour valeur V'i = 0.
Un paramètre b, choisi dans la suite des nombres premiers, est affecté à chaque vecteur O à mémoriser.
Exemple
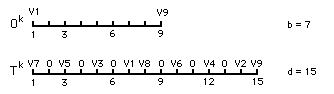
On mémorise T, on modifie d , b ne change pas, c'est la clé affectée au vecteur
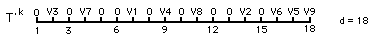
On obtient ainsi pour chaque vecteur Ok, k 1, ..., K, un ensemble de transformés de Ok, Tk, T'k, T''k,... de dimensions d ( m1, m2, .. , mM) différentes.
On fait de même pour chaque vecteur Ok, à mémoriser .
On additionne ensuite les vecteurs de même dimension d.
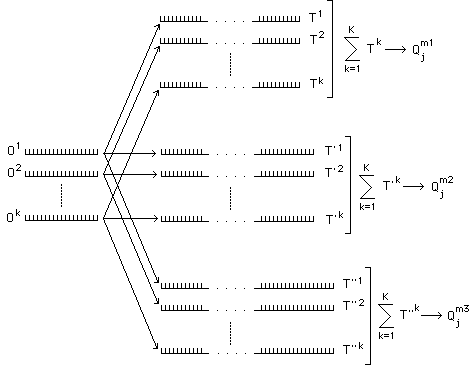
La j-ième composante d'un vecteur résultat, Qd, d1=m1, ..., D=mM est, pour une dimension d donnée
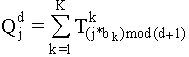
La variation de d va générer, pour chaque zone de stockage, un vecteur transformé différent. Un vecteur d'origine de clé "b" va donc être inscrit, sous forme de plusieurs vecteurs transformés, dans des "bruits" différents.
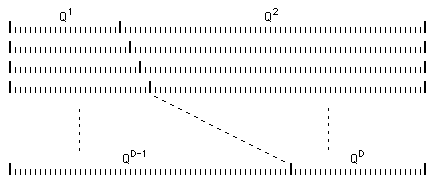
Les vecteurs sont associés par deux, la dimension de l'un diminue lorsque la dimension de l'autre augmente. La longueur résultante et le nombre (D) de vecteurs de stockage sont des paramètres du modèle.
1.3 phase de restitution
La restitution du vecteur à partir de ses transformés revient à extraire un signal d'un bruit.
Nous avons choisi une méthode dérivée de celle utilisée pour les potentiels évoqués: l'annulation du bruit est obtenue par moyennage de copies multiples du signal, chacune étant bruitée de façon différente.
Pour une clé donnée le vecteur de sortie est obtenu en faisant la moyenne des vecteurs transformés inscrits sur le réseau:
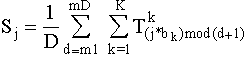
2- modèle avec modulation associée à la transformation chaotique
Le principe est le même que le précédent mais on introduit un traitement du signal avant ou au moment du stockage. Il s'agit d'une modulationmodulation d'amplitude par un signal sinusoïdal.
L'utilisation d'une modulation d'amplitude en radiophonie a pour but de décaler, dans le spectre des fréquences, la fréquence propre du signal à transmettre. Elle permet d'éviter la superposition des stations émettrices.
Y(t) = A(t).sin 2pi F.t
Y(t) est le signal modulé, A(t) le signal modulant, F la fréquence modulée ou porteuse.
Ici la modulation va avoir pour effet d'orthogonaliser plus encore les vecteurs à mémoriser, sans perte d'information, puisque la démodulationdémodulation restitue le signal d'origine.
La porteuse est générée par échantillonnageéchantillonnage d'une sinusoïde dont la période est un sous-multiple de la dimension des vecteurs transformés. En d'autres termes, on trouve un nombre entier de périodes dans chaque vecteur transformé.
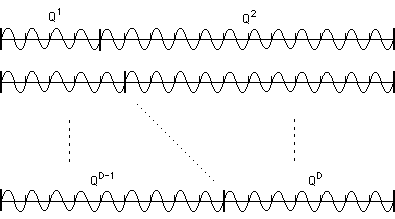
Le pas d'échantillonnage est égal au paramètre b qui est la clé affectée à chaque vecteur à mémoriser.
Quelques porteuses obtenues par échantillonnage de la sinusoïde de base:
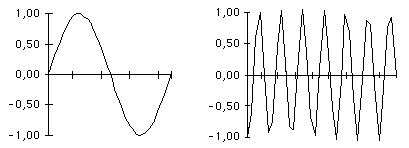
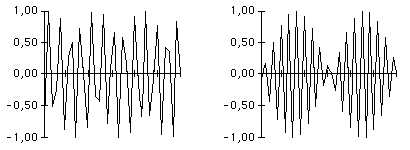
exemple de signal modulé obtenu avec b = 7
La figure suivante montre le gain obtenu en orthogonalisation pour un même vecteur, transformé avec des b premiers différents 5..51
Le gain en orthogonalisation reste faible pour la seule transformation chaotique mais celle-ci génère une modulation propre à chaque image qui se révèle très puissante.
Si nous prenons deux vecteurs différents à l'origine les vecteurs transformés deviennent quasi orthogonaux.
3- Etudes
3.1 capacité maximale théorique de stockage
L'opération de modulation est une méthode d'orthogonalisation. Nous l'avons comparée à la méthode de référence de GRAM SCHMIDT KEE.
Un premier vecteur à mémoriser est transformé avec une "clé" b en un ensemble de vecteurs chaotiques de dimensions d différentes (Q1 à QD). Cet ensemble constitue la base sur laquelle viendront s'additionner les ensembles suivants.
Un deuxième vecteur est transformé avec une clé différente et génère un deuxième ensemble de vecteurs chaotiques.
Si on veut additionner les deux ensembles de façon à ce que l'un apparaisse comme un bruit par rapport à l'autre, il faut orthogonaliser le deuxième ensemble par rapport au premier. C'était le rôle de la modulation dans notre méthode.
Dans la méthode de GRAMméthode de GRAM SCHMIDT l'ensemble est recalculé. Le coefficient à appliquer à chaque composante d'un vecteur transformé de dimension d donnée est mémorisé. Il permettra la reconstruction du vecteur d'origine en phase de restitution.
Les vecteurs suivants sont mémorisés de la même façon: chaque nouvel ensemble est recalculé de façon à être orthogonal aux éléments déjà mémorisés.
Dans notre expérimentation la méthode de GRAM SCHMIDT permet de doubler la capacité de stockage (20 vecteurs-tests à niveaux de gris au lieu de 10).
.
20 "images" mémorisées /
exemples restitution après superposition

3.2 activité du réseau
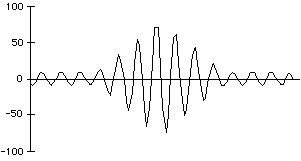
La figure ci-dessous montre les 100 premières valeurs des 4 premieres zones de stockage Qm1, Qm2, Qm3, Qm4, après l'inscription de 6 vecteurs transformés Tk k1.. 6
sur le réseau et la partie du vecteur somme correspondant. On remarque que les valeurs particulières à chaque image s'annulent et que le signal sinusoidal échantilloné au départ est reconstitué par addition des porteuses affectées aux images.