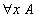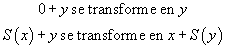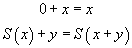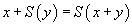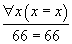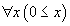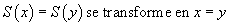
Questions

Question : Est-ce que la proposition 66 = 66 est dans la même classe que 65 = 65 ?

Réponse : Cela dépend des conventions. Si on prend la règle de calcul

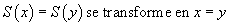
alors 66 = 66 se trouve être dans la même classe que 65 = 65, qui est lui-même dans la même classe que 0 = 0, et si on prend également la règle

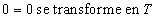
également dans la même classe que la proposition T. Mais, encore une fois, poser cette question est un peu la même chose que demander si l'hypothèse du continu est vraie ou fausse. La réponse dépend des conventions qu'on s'est fixées. On est aussi libre de choisir ses règles de calcul, que de choisir ses axiomes et ses règles de déduction.

Q : Combien y a-t-il de classes d'équivalences ?

R : Cela dépend encore des conventions, mais le système de déduction est indécidable, le nombre de classes est nécessairement infini.

Q : Les propositions A et « A et A » ont-elles même sens ?

R : Dans les exemples que j'ai donnés, j'ai commencé par des règles qui s'appliquaient à des termes, puis à des règles qui s'appliquaient à des propositions atomiques, on peut continuer en donnant des règles qui s'appliquent à des propositions composées. Dans ce cas, on peut choisir des règles de manière à ce que les propositions A et « A et A » aient même sens.

Q : Il semble y avoir une grande liberté dans le choix des règles ?

R : De la même manière qu'il y a un théorèmethéorème d'incomplétude qui montre que chaque fois qu'on a un système d'axiome, on peut l'enrichir, il y a un théorème d'indécidabilité qui montre que chaque fois qu'on a un ensemble de règles de calcul, il y a une proposition qui n'est pas établie par ce système de calcul et donc qu'on peut l'enrichir par de nouvelles règles de manière à établir cette proposition. De la même manière qu'il n'y a pas une vérité absolue indépendante des axiomes qu'on utilise pour raisonner, il n'y a pas de sens absolu indépendant des règles de calcul (de l'ensemble des transformations qui préservent le sens).

Q : Quel sens attribuer aux énoncés non démontrables ?

R : C'est vrai que si on dit A et B ont le même sens s'ils ont les mêmes démonstrations, alors deux énoncés non démontrables ont toujours même sens. Donc le petit théorème de Fermat et le grand théorème de Fermat n'ont pas le même sens, mais leurs négations si (si la théorie des ensembles est cohérente).

Une solution serait de dire que A et B ont le même sens si « être une démonstration de A » est intentionnellement égal à « être une démonstration de B ».
Deux propositions ont le même sens si l'intentionnalité d'être une démonstration de A et d'être une démonstration de B sont égales.
Mais ici, l'intentionnalité, ce n'est jamais qu'un autre nom pour le sens.
Cette définition est donc circulaire.

On peut alors dire que deux propositions ont le même sens si les démonstrations de A et les démonstrations de B sont les mêmes dans tous les systèmes d'axiomes. La manière dont on démontre une proposition dans tel ou tel système d'axiomes donne une indication sur son sens. Cela résout le problème pour les propositions indéterminées (par exemple, l'hypothèse du continu), mais pas pour les négations de propositions démontrables, par exemple les négations de tautologies, ces propositions ne sont démontrables que dans des systèmes incohérents, donc elles ont des démonstrations triviales dans tous les systèmes d'axiomes dans lesquels elles sont démontrables.

Pour ces propositions, je ne sais pas répondre autre chose que « posons par principe que deux propositions ont le même sens, si elles ont la même forme réduite ». Dans ce cas deux propositions qui ont le même sens ont les mêmes démonstrations, mais deux propositions peuvent avoir le même ensemble de démonstrations sans avoir le même sens. Cela dit, ce cas ne se produit que si cet ensemble de démonstrations est vide, c'est-à-dire quand les propositions ne sont pas démontrables.

Q : Peut-on dire que deux propositions ont le même sens s'il y a un algorithme qui transforme toute démonstration de l'une en une démonstration de l'autre ?

R : Oui, mais pas n'importe quel algorithme. Sinon toutes les propositions démontrables ont le même sens, car les fonctions constantes sont calculables.

Q : Est-ce qu'on peut dire que définir une logique par des règles de déduction et des règles de calcul revient à découper les sens en deux fragments : un sens qui se rapporte aux règles de déduction, qui confine aux situations d'indécidabilité qui est le sens qu'on ne peut pas réduire à du calcul et un sens mécanisable qu'on peut se permettre d'éliminer en quotientant les énoncés par un ensemble de règles de calcul approprié ?

R : Il me semble que le premier sens, c'est la dénotation. Si le petit théorème de Fermat et le grand théorème de Fermat sont tous les deux démontrables, ils ont la même dénotation. En revanche ils n'ont pas le même sens, car ils ne véhiculent pas la même information. Donc, avoir le même sens, ce n'est pas être équivalent logiquement. Le sens c'est quelque chose de plus fin et qui, me semble-t-il, relève uniquement du calcul. Si pour décider que deux propositions ont le même sens, il faut encore donner un argument, il ne me semble pas qu'on puisse dire qu'elles ont le même sens.

Q : Peut-on filer la métaphore pour dire qu'on a une esquisse d'un modèle de la compréhension dans la conversation qui consisterait à supposer chez celui qui écoute, une tentative de construire une démonstration de ce que dit l'autre, de construire le sens de ce que dit l'autre ?

R : Oui, mais cette reconstruction doit rester dans un cadre décidable. Si je dis « Charles Martel est le père de Pépin le bref et Pépin le bref est le père de Charlemagne, donc Charles Martel est le grand-père de Charlemagne », je suppose que tu sais que le père du père de quelqu'un c'est son grand-père. Mais si j'ai appris, il y a cinq minutes que la troisième guerre mondiale était déclenchée, et que je sais que je suis le seul à le savoir ici, je ne peux pas te parler en supposant que tu le sais. Il faut que je considère que ce qui est implicite dans ce que je dis, tu le sais ou que tu peux en reconstruire la démonstration en un temps borné. Il faut que nous soyons d'accord sur ce que nous reconnaissons comme implicite. Je ne peux supposer que tu sais des choses uniquement dans un cadre décidable. Quand on communique des démonstrations dans un système constitué de règles de déduction et de règles de calcul, l'implicite est exactement avec ce qui est traité par les règles de calcul.

Q : Si on admet cette idée que dans une certaine mesure on joue avec une notion de cadre, et que chaque interlocuteur tente de reconstruire les démonstrations de ce que dit l'autre, où est cette propriété de la logique, sur laquelle tu es resté très discret, et qui est la possibilité d'élimination des coupures ? Quand ces démonstrations que chacun construit, sont-elles mises en branle dans un processus de calcul ?

R : C'est quand on utilise l'opérateur de descriptions. Au lieu de dire « le nombre 4 », je dis « le prédécesseur de 5 », où le prédécesseur de x est défini comme l'unique nombre dont le successeur est x et je sais que tu connais une démonstration que tout entier relatif a un prédécesseur (ou bien parce que je t'ai communiqué cette démonstration, ou bien parce qu'elle est dans nos présupposés). Si tu veux connaître la valeur du nombre que j'ai désigné, il te faut éliminer les coupures.

Q : Mais je ne vais pas toujours faire cela, je vais me contenter de connaître une démonstration de la bonne facture de la définition du prédécesseur, et je vais continuer à utiliser l'expression « le prédécesseur de 5 ».

R : Si je te demande de mettre le prédécesseur de 5 francs dans un parcmètre, il faudra faire le calcul pour mettre 4 francs.

Q : Pour répondre à la question « Qu'est-ce qu'une logique ? », tu as très peu fait appel à la notion de validité.

R : J'ai compris la question « Qu'est-ce qu'une logique ? » comme « Comment peut-on définir la notion de vérité ? ». De ce point de vue, il ne me semble pas que la notion de validité dans un modèle (ou dans tous les modèles) soit pertinente, car cette définition présuppose une notion de vérité pour les jugements de la forme « la proposition A est valide dans le modèle M ». En revanche cette notion de validité est centrale pour l'étude de ces systèmes logiques (cohérence, indépendance, etc.). Elle est aussi centrale pour comprendre comment on peut axiomatiser les mathématiques avec la théorie des ensembles et continuer, malgré tout, à faire de la géométrie avec les axiomes d'EuclideEuclide : le théorème de complétude indique que les théorèmes de la géométrie d'Euclide peuvent se reformuler comme des théorèmes de la théorie des ensembles concernant les modèles de cette théorie.

Q : En utilisant la notion de dénotation, tu utilises pourtant une notion de vérité-correspondance.

R : Non, j'utilise une notion de vérité-démontrabilité. Je dis qu'une proposition a la dénotation « vrai » quand elle est démontrable et « faux » quand sa négation est démontrable. J'utilise aussi la notion de « avoir même dénotation que » pour dire « être prouvablement égal (ou prouvablement équivalent) à ». À aucun moment je ne suppose que toutes les propositions ont « vrai » ou « faux » pour dénotation.

Q : Mais Frege définit la notion de sens d'un énoncé comme les conditions auxquelles cet énoncé dénote le « vrai » (au sens de la vérité-correspondance).

R : C'est pour cela que je me suis référé à la définition donnée par Dummett du sens comme comme conditions d'assertabilité (de démontrabilité) et non à la définition originale de Frege.

Q : La définition du sens que tu as utilisée est assez différente de celle de Frege, également parce que, pour Frege 2⁴ et 4² ont la même dénotation, mais pas même sens, car le mode de donation de l'objet n'est pas le même. Même s'il y a quelque chose de plus proche entre 2⁴ et 4² qu'entre 2⁴ et n'importe quelle autre définition du même objet.

R : Si on suppose que 2⁴ et 4² ont des sens distincts, je ne vois pas ce qui pourrait avoir même sens que 2⁴, si ce n'est l'expression 2⁴ elle-même. Si pour avoir même sens, deux expressions ou deux propositions doivent avoir exactement le même mode de donation, « avoir même sens » devient synonyme de « être la même expression ». Dans ce cas la notion de sens n'apporte plus grand chose. L'égalité de sens me semble être intermédiaire entre l'égalité de dénotation et l'égalité syntaxique.

Q : Cela dit, on peut penser que dans certaines situations 2⁴ et 4² ont le même sens, et dans d'autres non, puisque ce qui est implicite peut varier en fonction des interlocuteurs.

R : Oui.

Q : Cette démarcation entre ce qui est vrai par le calcul et ce qui demande une démonstration peut se comparer avec la démarcation des propriétés d'anneau des entiers relatifs au sein de toutes leurs propriétés.

R : Oui, dans les deux cas on isole un sous-ensemble des connaissances qu'on utilise.

Q : Il y a une stratégie de la démarcation entre calcul et déduction. On pose la ligne de démarcation pour certaines raisons.

R : Oui, on cherche à pousser la démarcation le plus loin possible. Mais on peut toujours la pousser encore un peu.

Q : Parmi toutes ces connaissances, quelles sont celles qui sont justiciables d'un traitement par le calcul ?

R : Il y a l'élimination des coupures, ce qui fait déjà pas mal de choses.