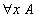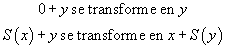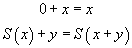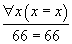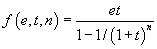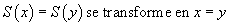au sommaire
Le calcul et le raisonnement
On aimerait, quand on utilise ce type de techniques, avoir la possibilité de poser des questions générales comme « est ce que
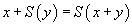
qu'on ne sait pas traiter autrement que par la recherche d'une démonstration, mais aussi garder l'efficacité habituelle des ordinateursordinateurs pour résoudre les problèmes simples. On ne veut donc pas abolir la différence entre le calcul et le raisonnement.
Cette idée a été très bien formulée par Gordon Plotkin en 1972 (G. Plotkin, Building-in equational theories, Machine IntelligenceIntelligence, 7 (1972) p. 73-90) quand il a remarqué qu'avec l'unique axiome
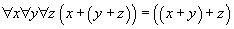
un programme de démonstration automatique passait une grande partie de son temps à réarranger les parenthèses dans un sens ou dans l'autre sans rien produire d'intéressant.
L'idée est donc de ne pas abandonner cette notion de calcul dans la définition d'une logique. En arithmétique, par exemple, on garde les deux règles :
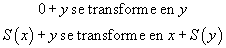
On étend leur utilisation en les appliquant aux propositions, ce qui permet de dire non seulement que le terme 9 + 57 se réduit sur le terme 66, mais également que la proposition 9 + 57 = 66 se réduit sur la proposition 66 = 66. De même, la proposition 9 + 57 = 65 se réduit sur la proposition 66 = 65. On peut alors quotienter l'ensemble P des propositions par la relation avoir la même forme réduite. On identifie ces deux expressions en les considérant comme représentantes d'un objet plus général : l'ensemble des propositions qui ont la même forme réduite qu'elles. Une formulation équivalente consiste à dire qu'on démontre uniquement des propositions réduites, et que 9 + 57 = 66 n'est pas une proposition, mais une pré-proposition qui se calcule en 66 = 66.
Quand on demande à un ordinateur de démontrer la proposition 9 + 57 = 66, il commence par réduire cette proposition en 66 = 66. Cette proposition a une démonstration beaucoup plus simple : il suffit d'appliquer le principe d'identité, c'est-à-dire l'axiome
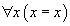
Appliquer les règles de calcul pour réduire la proposition 9 + 57 = 66 et obtenir 66 = 66 a naturellement un coût, mais ce coût est bien moindre que celui de l'exploration de toutes les possibilités dans le cas de la recherche d'une démonstration en arithmétique.
Que devient alors l'axiome
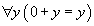
En l'absence de règles de calcul, on avait besoin de cet axiome pour démontrer la proposition 9 + 57 = 66. Quand on ajoute les règles de calcul, cette proposition se démontre par le principe d'identité, et cet axiome n'est plus nécessaire. Il semble y avoir une redondance entre l'axiome et la règle de calcul. En fait l'axiome lui-même est un représentant de sa forme réduite
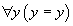
De même l'axiome
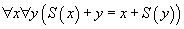
est un représentant de sa forme réduite
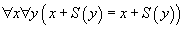
Ces axiomes, qui sont conséquences du principe d'identité, peuvent être supprimés.
Donnons quelques exemples de règles : en arithmétique, on a les deux règles déjà données et des règles similaires pour la multiplication. Si on peut transformer non seulement les termes mais aussi les propositions, on peut ajouter les règles :
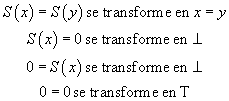
Le troisième et le quatrième axiome de Peano
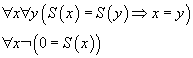
deviennent superflus puisqu'ils se transforment en
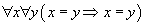
et
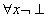
qui sont des théorèmes du calcul des prédicats. Seul le schéma de récurrence reste comme axiome.
Un autre exemple est la règle de calcul de l'associativité
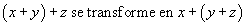
Dans certaines formulations de la théorie des ensembles l'axiome
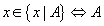
peut être remplacé par la règle

Dans les formalisations des mathématiques qui s'appuient, non sur la notion d'ensemble, mais sur celle de fonction, on note
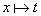
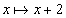
On peut alors remplacer l'axiome
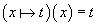
par la règle
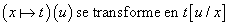
Dans toutes ces théories, ajouter ces règles permet de supprimer des axiomes et de rendre les démonstrations plus courtes puisque certains arguments calculatoires en sont supprimés. On distingue ainsi le calcul qui est pris en charge par ces règles, du raisonnement qui reste dans les démonstrations formelles qui sont plus courtes, plus informatives et plus faciles à trouver.