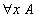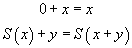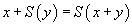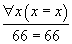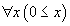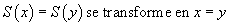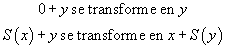
Le calcul

Bien avant de savoir construire un raisonnement, nous savions déjà faire des additions (par exemple, ajouter 9 et 57)).
Faire une addition sur des nombres en notation décimale demande une technique assez sophistiquée. Une méthode plus simple consiste à noter le nombre 9 par neuf bâtons et 57 par cinquante sept bâtons :

|||||||||+|||||||||||||||||||||||||||||||||||||||||||||||||||||||||

et pour faire l'addition, on efface alors un à un les bâtons à gauche du signe + en en ajoutant un à droite chaque fois

||||||||+||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Quand il ne reste plus de bâtons à gauche

+||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

on peut effacer le signe + et on obtient le résultat : 66

||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Ce type d'expressions peut s'écrire dans un langage du premier ordre, avec un symbole zéro (0) et un symbole successeur (S) et les règles que nous avons utilisées pour effectuer l'addition peuvent se traduire comme des règles de transformation sur les termes de ce langage :

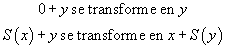
On peut dire que ces règles sont des règles de calcul, car partant de n'importe quel terme, par exemple le terme 9 + 57, en appliquant ces règles un certain nombre de fois, on finit par obtenir un terme, par exemple 66, auquel aucune règle ne peut plus s'appliquer. Ceci est une propriété de terminaison. Il est, par exemple, impossible d'avoir une règle

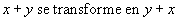
puisque 0 + 1 pourrait se transformer en 1 + 0 qui se transforme en 0 +1, et ce à l'infini. Avec ce type de règles on sort donc du cadre du calcul.

L'autre propriété qui définit le calcul, la confluence, consiste à dire que quelle que soit la manière dont on applique les règles, s'il s'avère que deux règles peuvent s'appliquer en même temps, elles mènent, au bout du compte, au même résultat. Par exemple, on ne peut pas avoir deux règles

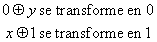
Le terme

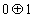
se transformerait à la fois en 0 par la première règle et en 1 par la seconde. Ici, on est encore sorti du cadre du calcul car on a deux résultats pour le terme de départ. Ces propriétés de terminaison et de confluence impliquent que chaque terme se réduit en une forme unique, l'existence est une conséquence de la propriété de terminaison et l'unicité de la confluence.