au sommaire
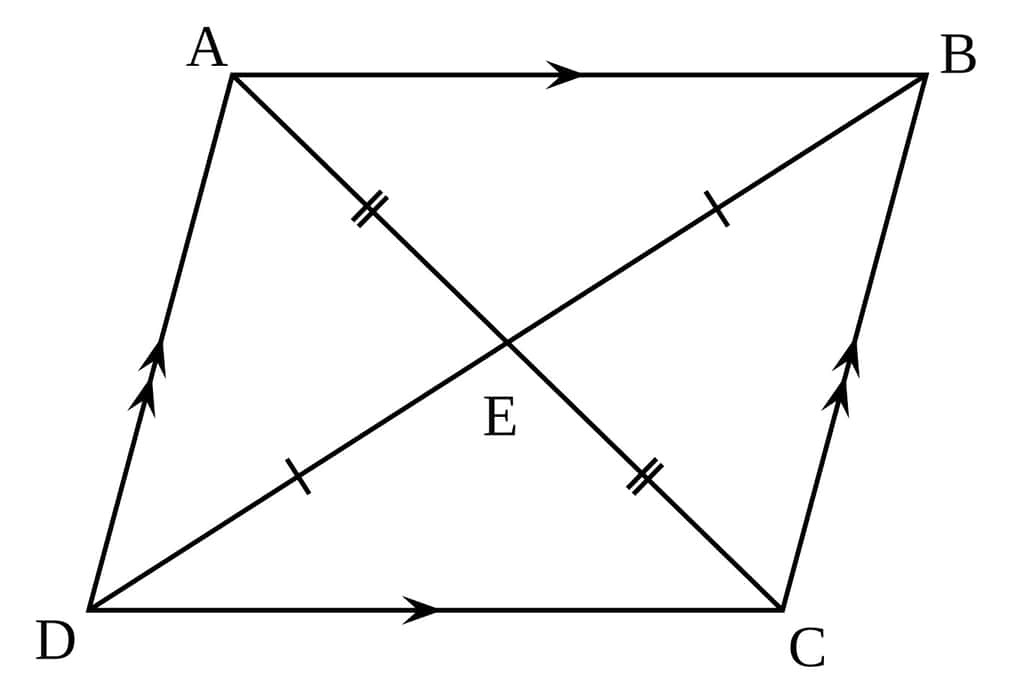
Le parallélogramme est une figure de géométrie définie par quatre côtés opposés deux à deux parallèles. Sa caractéristique principale réside dans le fait que les côtés opposés sont de même longueur et les angles opposés sont égaux. Un parallélogramme ABCD aura ainsi ses côtés AB parallèles à DC et AD parallèles à BC, soit AB // DC et AD // BC.
Un aspect remarquable du parallélogramme est également la somme des angles internes, toujours égale à 360 degrés. Cette symétrie et ces relations entre côtés et angles en font une figure clé dans la géométrie euclidienne.
Caractérisation et preuves mathématiques
Pour prouver qu'un quadrilatère est un parallélogramme, il faut qu'il remplisse au moins une des conditions suivantes :
- Côtés opposés parallèles
- Côtés opposés de même longueur
- Angles opposés de même mesure
- Diagonales qui se coupent en leur milieu
- Le centre de symétrie du parallélogramme est le point d'intersection de ses diagonales
- Les angles consécutifs sont supplémentaires (leur somme est égale à 180°)
Cas particuliers notables des parallélogrammes
Dans la famille des parallélogrammes, on trouve des cas particuliers qui possèdent des propriétés distinctes.
- Le rectangle, par exemple, est un parallélogramme avec quatre angles droits, avec des diagonales de même longueur et des côtés consécutifs perpendiculaires.
- Le losange, lui, est caractérisé par des diagonales perpendiculaires et quatre côtés de même longueur.
- Le carré est un cas particulier puisqu'il est à la fois un parallélogramme, un rectangle et un losange, combine les propriétés des deux derniers, avec des côtés égaux et des angles droits.
Calcul de l’aire d’un parallélogramme
Pour calculer l'aire d'un parallélogramme, voici une formule simple : en multipliant la longueur de la base par la hauteur perpendiculaire à cette base, on obtient l'aire. Mathématiquement, cela se traduit par A = b x h, où A est l'aire, b représente la longueur de la base, et h est la hauteur. La hauteur est la distance perpendiculaire entre la base choisie et la droite parallèle la plus éloignée.
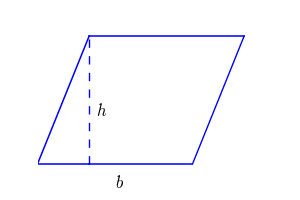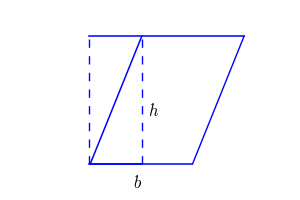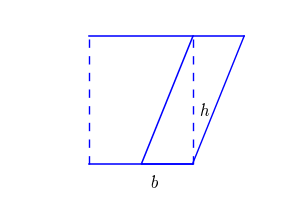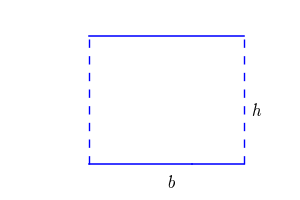
La formule pour calculer l'aire d'un parallélogramme est : Aire = (base × hauteur).
Applications pratiques des parallélogrammes
Bien au-delà des salles de classe et des manuels de géométrie, les parallélogrammes trouvent une multitude d'applications dans le monde réel. Par exemple, dans l'architecture et le génie civil, ils sont utilisés pour concevoir des structures et des charpentescharpentes qui nécessitent des éléments structurels non perpendiculaires. Les parallélogrammes contribuent également à la conception de machines et de mécanismes, comme des articulationsarticulations et des systèmes de levage qui exploitent les propriétés uniques des angles et des côtés de ces figures pour une efficacité optimale.
