au sommaire
À la base de tous les grands accélérateurs de particules, on trouve des champs électriques augmentant lentement mais sûrement la vitesse des protons, électrons ou ions utilisés pour effectuer des collisions. Le cas le plus simple est celui où l'on fait passer un électron dans une région où règne une différence de potentiel entre deux plaques électriquement chargées. Plus la différence de potentiel est grande, plus la vitesse atteinte par les particules est élevée. Cette différence est donnée en gros par le produit de l'intensité du champ électrique entre les plaques par la distance qui les séparent. On comprend donc que pour accélérer des électrons presque à la vitesse de la lumièrevitesse de la lumière, il faut soit les faire voyager sur une longue distance avec un champ électrique faible, soit sur une courte distance avec un champ électrique fort.
Dans le premier cas, on peut placer en série des cavités avec deux plaques électriquement chargées sur une longue distance. C'est le cas de l'accélérateur linéaire de Stanford, le fameux Slac où s'est illustré le prix Nobel Burton Richter. Mais on peut aussi, et c'est ce qui avait été fait avec les premiers cyclotronscyclotrons et ensuite avec le collisionneur LEP, s'arranger pour faire tourner en cercle un paquetpaquet de particules chargées pour les faire passer à plusieurs reprises dans la même région où règne une différence de potentiel.
Mais quand la trajectoire est courbe, les particules chargées se mettent à rayonner d'autant plus fortement, et donc à perdre de l'énergieénergie et de la vitesse, que la courbure de la trajectoire est élevée.
Les contraintes de l'accélération des particules chargées
La puissance rayonnée par une particule sur une trajectoire incurvée dépend aussi de l'inverse de la puissance quatrième de la massemasse de la particule accélérée. La masse d'un proton étant presque 2.000 fois supérieure à celle d'un électron, on comprend pourquoi il vaut mieux utiliser tout à la fois un accélérateur de protons circulaire d'un grand diamètre qu'un petit accélérateur circulaire d'électrons pour faire des expériences à hautes énergies. C'est d'ailleurs ce que l'on fait au LHC pour atteindre des énergies de 7 TeV lors des collisions.
Il y a un autre problème dont il faut tenir compte dans la course aux hautes énergies. Si l'on fait entrer en collision un faisceau de particules avec une cible fixe, seule une petite partie de leur énergie peut se transformer en de nouvelles particules. Il vaut donc mieux, et de très loin, faire entrer en collision deux faisceaux de particules. Là aussi cela explique pourquoi le LHCLHC est un collisionneur à deux faisceaux de protons.
Une vidéo expliquant certains des principes des accélérateurs de particules. © Cern
Toutefois, pour étudier la physiquephysique des hautes énergies, il ne suffit pas de monter à des énergies de plus en plus hautes. Il faut que le signal des nouvelles particules dans les détecteurs ne soit pas trop brouillé par le déluge des particules déjà connues. Malheureusement, cela n'est pas particulièrement le cas avec des hadronshadrons.
Des mesures fines ne pourront donc être réalisées qu'avec un accélérateur utilisant des électrons à hautes énergies. De ce qui précède on comprend que si l'on veut étudier avec précision des particules dont les masses sont de l'ordre de 1 TeV, il faudra impérativement utiliser des collisionneurs de faisceaux d'électrons et de positronspositrons accélérés par des cavités disposées linéairement. Tout le problème est de construire ces cavités et de réduire au maximum les contraintes technologiques et financières en trouvant le moyen de créer des champs électriques les plus intenses possibles.
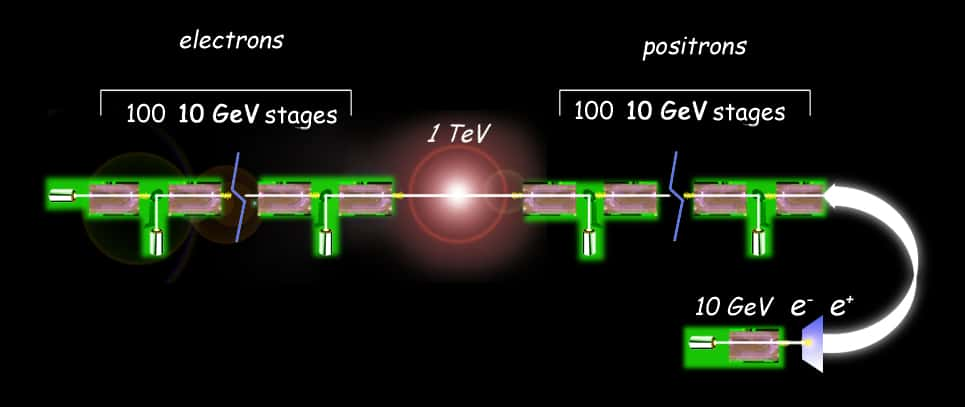
Le schéma d'un futur collisionneur linéaire avec deux accélérateurs linéaires utilisant des éléments d'accélération avec laser et plasma. © Lawrence Berkeley National Laboratory
Il y a environ trente ans, John Dawson et Toshiki Tajima ont eu l'idée d'utiliser pour cela des ondes électromagnétiquesondes électromagnétiques dans des plasmas induites par des impulsions laserslasers. Pour comprendre de quoi il retourne, on peut prendre l'image d'un puissant hors-bord créant une vague emportant au passage un surfeur dont la vitesse augmente alors. Le passage de l'impulsion laser dans un plasma va induire des différences de potentiel électrostatiqueélectrostatique telles qu'il est en théorie possible d'obtenir des électrons avec des énergies de 10 GeVGeV en les accélérant sur une distance de l'ordre du mètre.
En théorie, une série de cavités accélératrices de ce type disposée sur une distance d'une centaine de mètres devrait permettre d'obtenir des faisceaux à des énergies de l'ordre d'un TeV, c'est-à-dire 1.000 GeV. Pour mémoire l'accélérateur linéaire de Stanford, avec ces 3,2 kilomètres de long, ne permet d'atteindre que des énergies de l'ordre de 50 GeV. Le collisionneur qui le prolonge permet ensuite d'atteindre des énergies de l'ordre de 90 GeV dans les collisions.
Depuis plusieurs années, des chercheurs du U.S. Department of Energy's Lawrence Berkeley National Laboratory travaillent précisément à la réalisation d'un tel accélérateur linéaire avec le Berkeley Lab Laser Accelerator (Bella).
Einstein à la rescousse
Malheureusement, sa conception nécessite de réaliser des simulations en 3D extrêmement gourmandes en temps de calcul. Surtout, les chercheurs étaient confrontés à des problèmes d'instabilités numériquesnumériques (à ne pas confondre avec les instabilités des systèmes dynamiques chaotiques). En effet, tout comme pour le cas des calculs de la masse du proton et d'autres hadrons à l'ordinateurordinateur, il faut discrétiser en temps et en espace les équationséquations aux dérivées partielles décrivant le plasma couplé aux impulsions lasers. On réalise donc des calculs utilisant un petit intervalle de temps pour les pas de calculs et sur une sorte de réseau spatial cristallin avec une distance donnée entre les points du réseau. Ce qui soulève une grosse difficulté. Pour augmenter la précision des calculs, il faut en effet considérer des intervalles de temps et d'espace de plus en plus petits. Or, ce faisant, les calculs résultant peuvent se mettre à diverger fortement par rapport à leur véritable valeur. C'est en gros ce qu'on entend par instabilité numérique.
La parade a été trouvée par Jean-Luc Vay et ses collègues. Il suffit de se placer dans un référentielréférentiel se déplaçant presque à la vitesse de la lumière dans le cadre de calculs effectués par un superordinateursuperordinateur. Numériquement parlant, les effets de la relativité restreinterelativité restreinte d'EinsteinEinstein se manifestent pour un observateur se déplaçant à une vitesse proche de celle des impulsions lasers dans le plasma. La dilatation du temps ralentit les processus d'oscillations dans le plasma tandis que celle de Fitzgerald-Lorentz contracte les distances spatiales.
Dans un tel référentiel, il n'est donc plus nécessaire d'utiliser des intervalles d'espace et de temps de très faibles valeurs pour obtenir la précision demandée. Surtout, des simulations de processus de longues duréesdurées et se déroulant sur de grandes distances dans le référentiel au repos, et donc demandant un grand nombre de pas de calcul, se réduisent à des durées et des distances courtes. Il suffit de transformer les résultats obtenus dans le référentiel allant presque à la vitesse de la lumière dans celui du laboratoire pour obtenir la simulation de Bella demandée.
De cette manière les chercheurs ont réalisé en quelques heures seulement des calculs qui défiaient les superordinateurs il y a seulement deux ans, réduisant les temps de calculs par un facteur de l'ordre de plusieurs dizaines de milliers. Mieux encore, on obtient ainsi un résultat en 3D, alors qu'une simulation à une dimension demandait auparavant 5.000 heures calculs.