au sommaire

Srinavasa Varadhan, prix Abel 2007.
Brève présentation de S. Varadhan
Né en 1940 à Chennai (Inde), S. Varadhan soutient sa thèse de doctorat en 1963, avec parmi les auditeurs le célèbre mathématicienmathématicien russe Kolmogorov, invité pour l'occasion par le professeur Rao. S. Varadhan commence en tant que post-doctorant au Courant Institute of Mathematical Sciences à New-York, et il y restera fidèle, obtenant un poste de professeur en 1972 et celui de directeur en 1980 (à la suite de Peter Lax, prix Abel 2005). Entre autres distinctions, le professeur indien s'est vu attribué le prix Birkhoff (1994), le Prix Margaret et Herman Sokol (1995), et le Prix Leroy Steele (1996). Il est aussi docteur honoris causa de l'Université Pierre et Marie CurieMarie Curie de Paris (2003) et membre de plusieurs sociétés savantes, dont la US National Academy of Sciences (1995) et l'Indian Academy of Sciences (2004). Nous renvoyons le lecteur à la biographie de S. Varadhan, rédigée par la fondation Abel, pour plus de détails.
Pile ou face ? Le « principe des grandes déviations » sur un exemple
Au jeu de « pile ou face », il est assez intuitif d'imaginer que le nombre de fois où la pièce tombe côté pile représentera environ 50% des cas, pourvu que le nombre de tirages soit suffisamment grand. C'est la loi des grands nombres, figurée par Pascal et énoncée par Jacob Bernoulli au début du XVIIIème siècle, qui stipule qu'en répétant un grand nombre de fois une expérience, chacune des issues possibles se produit en raison de sa probabilité d'occurence. Si l'on note Rn la proportion de « pile » apparus pour une série de n tirages, on peut donc écrire que
ce qui signifie que la probabilité pour que cette proportion soit de 50% est aussi proche de 1 que le nombre de tirages augmente.
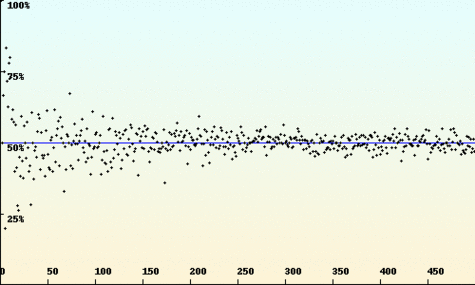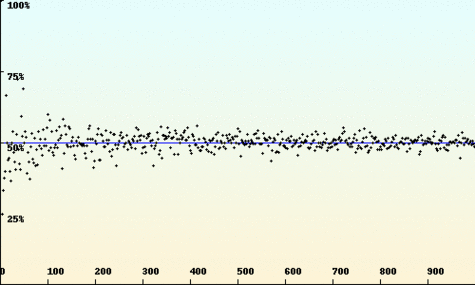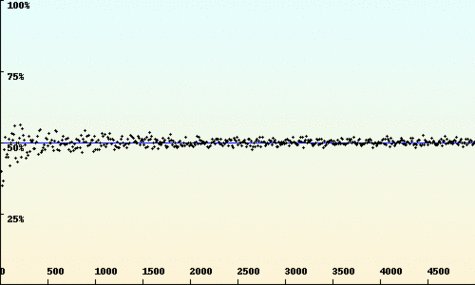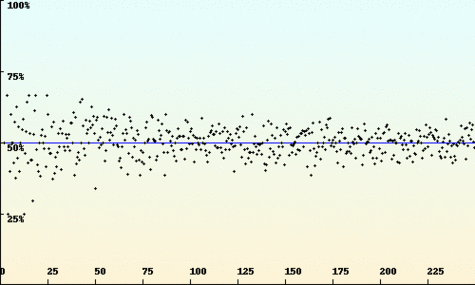
La loi des grands nombres : chaque point représente la proportion d'issues « pile » pour une série de n tirages à pile ou face (où n est porté en abscisse). Cette proportion est d'autant plus proche de 50% que le nombre de tirages est grand.
Crédits : S Tummarello.
Un corollaire immédiat est que la probabilité de trouver une proportion de « pile » de 30% ou de 95% est d'autant plus minime que n augmente. La question se pose alors de savoir à quelle vitesse cette probabilité décroît. Un calcul direct montre que la probabilité de constater exactement k fois l'occurence « pile » sur n tirages vaut :
1 2^n . frac n! k!(n-k)!" alt=" " />.
En notant r la proportion attendue et en faisant usage de la formule de Stirling, on peut en déduire que
-nI(r) " alt=" " />
où I(r) est une fonction de r, ici égale à . C'est cette « fonction de taux » qui mesure la vitesse avec laquelle la probabilité diminue, et cette vitesse est bien nulle pour la « valeur typique » de 50%.
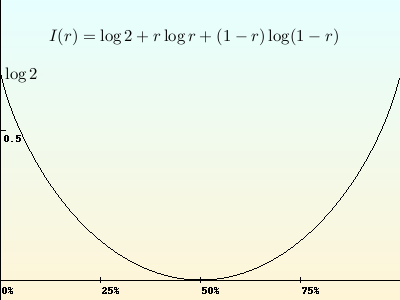
La fonction de taux I(r), associée au jeu de « pile ou face », mesure la vitesse avec laquelle la probabilité de trouver un certain pourcentage de « pile » décroît.
Crédits : S Tummarello.
Le principe des grandes déviations repose précisément sur l'existence d'une telle approximation -nI(r) " alt=" " />, et nous verrons que les fonctions de taux I(r) portent avec elles de nombreuses informations sur le système. Mentionnons dès maintenant que l'existence d'un unique zéro (pour r=50% ici) correspond rigoureusement à la loi des grands nombres.
Le théorème central limit et les grandes déviations
Toujours au même jeu, en convenant que l'on gagne un euro si l'on obtient « pile », et que l'on perd un euro sinon, la loi des grands nombres nous indique donc que l'espérance de gain est nulle (en dépit du fait que les parties peuvent engendrer alternativement des gains et des découverts importants). Cependant, le théorème « central limit » (deviné par de Moivre et Laplace, démontré par Gauss) permet d'estimer les possibilités de gain au bout d'un certain nombre n de tirages : plus n est grand, plus la loi de probabilité ressemble à la fameuse distribution de Gauss (la « courbe en cloche »).
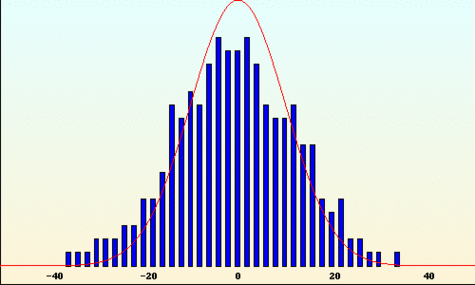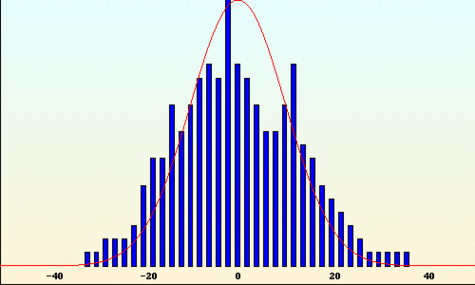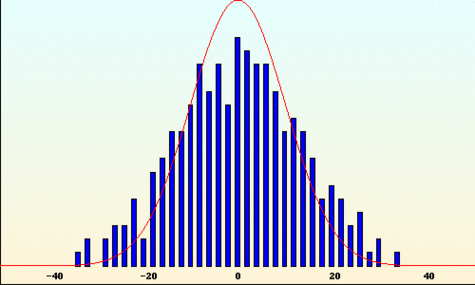
Probabilités de gain constatées pour 1000 séries de 200 tirages : en rouge la densité de probabilité limite, la célèbre gaussienne.
Crédits : S. Tummarello
Mais en 1937, le statisticien suédois H. Cramér découvre, en analysant pour des compagnies d'assurance des problèmes similaires de « ruine », que l'approximation de Gauss est trompeuse pour de grandes déviations par rapport à la moyenne. Ceci se comprend en examinant la fonction de taux I(r) : si elle admet une approximation quadratique autour de la valeur typique rtyp
12, I^''left( r_ rmtyp right), . , left( r-r_ rm typ right)^2" alt=" " /> (développement de Taylor),
ce qui fournit en retour le théorème central limit, cette approximation n'est en général valable que pour des « petites déviations ». Pour les grandes déviations, puisque l'approximation gaussienne perd de sa pertinence, la méthode consiste à calculer et étudier directement la fonction I(r), pourvu qu'elle existe (d'où le principe des grandes déviations).
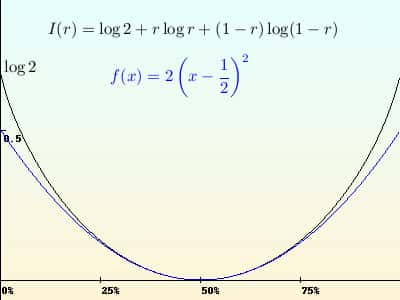
La fonction de taux I(r), et son approximation quadratique autour de 50% (en bleu) : pour des grandes déviations, cette dernière cesse d'être correcte.
Crédits : S Tummarello.
Le chef-d'œuvre de Srinavasa Varadhan
Près de trente ans après Cramér, S. Varadhan a reformulé le problème des grandes déviations dans un cadre conceptuel révolutionnaire, où les fonctions de taux s'interprètent spontanément comme solutions d'équations découlant d'un principe variationnel élégant (minimisation d'une certaine « distance d'entropieentropie »). Une série d'articles, rédigés avec la coopération de Monroe D. Donsker, ont révélé la puissance de cette approche nouvelle, qui a permis de clarifier et d'unifier une grande variété de phénomènes complexes, et qui depuis s'est distinguée comme la clef de voûte de cette branche des probabilités.
Pour en savoir plus sur ce sujet et sur les autres contributions majeures de S. Varadhan, le lecteur est invité à consulter le communiqué de la fondation Abel.