au sommaire
Transformation chaotique d'un vecteur et applications
1. Généralités
La transformation proposée transforme un vecteur quelconque de dimension n en un "vecteur chaotique" de même dimension, c'est à dire en un vecteur dont les composantes ont été permutées de façon pseudo-aléatoire grace à un algorithme d'étirement-repliement qui génère une suite chaotique de nombres. Cette transformation est réversibleréversible.
2. Transformation d'un vecteur en un vecteur chaotique
Si on décrit un vecteur comme une suite de n composantes Ci de valeur Vi.
Chaque composante a une position Ai.
Le vecteur d'origine peut s'écrire:
C1, Ci .... ,Cn de valeurs V1,Vi ....... ,Vn
i 1.. n
La transformation va porter sur la position des composantes successives du vecteur :
la suite des positions va subir une permutation qui va délocaliser les composantes d'origine tout en conservant leur valeur.
Pour chaque composante Ci d'adresse Ai, on va calculer une nouvelle adresse A'i qui correspondra à la position de cette composante dans le vecteur transformé.
A'i = i * b modmod (n+1)
i 1..n
b premier par rapport à (n+1)
Si on calcule l'adresse A'i à partir de l'adresse A'i-1, la suite des A'i peut s'écrire:
A'i = (A'i-1 + b) mod (n+1)
A'0 = 0
i 1.. n
b premier par rapport à (n+1)
On remarque que cette suite est de la forme
A'i = (a * A'i-1 + b) mod (n+1)
a = 1
i 1.. n
b premier par rapport à (n+1)
Cette formule a pour particularité de générer la suite des nombres de 1 à n dans un ordre chaotique DEW87. Pour n donné, cette suite est différente pour chaque valeur du paramètre b, à ceci près qu'apparaissent des récurrences lorsque le nombre de permutations possibles est atteint (n-1). De façon classique pour un algorithme d'étirement-repliement le vecteur d'origine réapparait lors des récurrences (voir exemples Excel).
3. Exemples
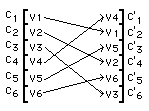
A- valeur de b inférieure à n+1: b = 3 et n = 6,
le vecteur transformé
C'1, C'2, C'3, C'4, C'5, C'6
est obtenu par une permutation des composantes du vecteur d'origine:
A'2 = (2*3) mod 7 = 6
A'3 = (3*3) mod 7 = 9-7 = 2
A'4 = (4*3) mod 7 = 12-7 = 5
A'5 = (5*3) mod 7 = 15-7*2 = 1
A'6 = (6*3) mod 7 = 18-7*2 = 4
B- valeur de b supérieure à n+1: b = 23 et n = 6,
A'1 = (1*23) mod 7 = 23-7*3 = 2A'2 = (2*23) mod 7 = 46-7*6 = 4
A'3 = (3*23) mod 7 = 69-7*9 = 6
A'4 = (4*23) mod 7 = 92-7*13 = 1
A'5 = (5*23) mod 7 = 115-7*16 = 3
A'6 = (6*23) mod 7 = 138-7*19 = 5
visualisons cette dernière transformation:

4. Matrice de transformation
Cette transformation vectorielle est une permutation qui est caractérisée par une matrice de permutation n x n (P) construite à partir de la séquence chaotique correspondant à un paramètre b donné.
exemple avec b = 3:
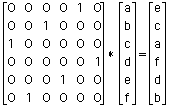
5. Transformation inverse
La tranformation est biunivoque et la transformation inverse s'obtient en multipliant le vecteur transformé par la matrice inverse.
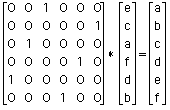
Maintenant que l'on a pu voir le principe d'une telle transformation, tâchons d'en voir l'utilité à travers plusieurs exemples, à commencer par le stockage d'informations sur une structure en boucle
Vous pouvez aussi télécharger des exemples au format
- Excel IV : Matrices de permutation / Récurrences
- Excel V : Brouillage d'un texte
Retrouvez également sur le site de l'auteur du sujet d'autres exemples illustrés tels que :
* Prétraitement d'image avant stockage sur mémoire associative



















