au sommaire
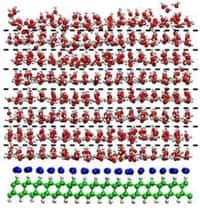
La structure de la glace hexagonale et les molécules d'eau pour de la glace en train de fondre. Crédit : Davide Donadio–ETH Zürich
Une des difficultés les plus importantes de la physique est ce que l'on appelle le problème à N corps. Il s'agit de comprendre et de prédire ce qui se passe quand N particules exercent les unes sur les autres un ensemble de forces. On le trouve dans différentes disciplines comme la dynamique des planétésimaux lors de la formation du système solaire, le comportement des nucléons dans un noyau ou encore celui des électrons dans un matériau conducteur, voire supraconducteursupraconducteur.
Les possibilités analytiques de l'esprit humain étant ce qu'elles sont, une résolutionrésolution rigoureuse des équationséquations de mouvementsmouvements d'un problème à N corps n'est pas à sa portée. En fait, Poincaré a même montré, dans le cas de la mécanique céleste newtonienne, que le problème n'avait pas de solutions analytiques avec seulement trois corps. Jusque vers le milieu du vingtième siècle, les physiciensphysiciens cherchant à tirer quelques informations sur le comportement des moléculesmolécules d'un gazgaz ou d'un liquideliquide devaient s'en remettre aux méthodes de la mécanique statistique.

De gauche à droite Stanilas Ulam, Richard Feynman et John Von Neuman à Los Alamos. Crédit : AIP
Tout a changé avec la réalisation des premiers ordinateursordinateurs à partir des travaux de Turing et Von Neuman. Stimulés par les problèmes de mise au point des armes nucléaires, les physiciens ne tardèrent pas à résoudre numériquement des équations de systèmes à N corps. Une des premières simulations ayant donné un résultat non trivial est la célèbre simulation de Fermi, Pasta et Ulam, avec une série d'oscillateurs non linéaires couplés. On avait découvert à cette occasion une violation du théorèmethéorème de l'équipartition de l'énergieénergie et l'apparition, inattendue, d'un comportement lié à l'existence de ce qui sera appelé plus tard des solitonssolitons.
On sait que l’eau est un des liquides les plus mystérieux de l’Univers. Qu'arrive-t-il donc précisément dans le processus de fusionfusion de la glace ?
L'eau, un bon modèle pour le problème à N corps
Pour le savoir, Carl Caleman et David van der Spoel ont simulé sur ordinateur des «instantanés» de la fontefonte des cristaux de glace chauffés initialement par une brève impulsion de lumièrelumière produite par un laserlaser infrarougeinfrarouge.
Il faut savoir que ce qu'on appelle des simulations de dynamique moléculaire sont idéales pour obtenir une meilleure compréhension des processus comme ceux de la fusion ou de congélation de l'eau. Ils permettent en effet de décrire simultanément à la fois la structure et la dynamique d'un système à la résolution atomique et avec une résolution temporelle de l'ordre de la femtosecondefemtoseconde (10-15 s).
Les molécules d'eau dans la glace s'organisent en général pour former de la glace hexagonale. Sous cette forme, les atomesatomes d'oxygèneoxygène des molécules d'eau sont disposés en un réseau cristallinréseau cristallin tétraédrique. Chaque molécule d'eau est liée à quatre voisines par des liaisons hydrogèneliaisons hydrogène, avec une moyenne de deux liaisons par molécule. Dans l'eau, il y en a en moyenne seulement 1,75.
En rouge, la brève impulsion laser au début de la simulation. Crédit : Carl Caleman et David van der Spoel
La simulation a montré qu'en réponse à l'impulsion laser, les groupements OH des molécules d'eau vibrent en premier. L'énergie stockée sous forme vibratoire atteint rapidement un maximum et après environ une picosecondepicoseconde, celle-ci a été transformée en énergie de rotation et de translationtranslation, ce qui provoque la fusion de la glace, même si la structure hexagonale des domaines cristallins reste visible assez longtemps, comme le montre la vidéo ci-dessus.
On remarque ainsi que les molécules commencent à tourner et à s'écarter de leurs positions initiales au sein du cristal, brisant les liaisons hydrogène.
Après environ 3 à 6 picosecondes, les rotations diminuent en faveur des mouvements de translation. Les molécules sont maintenant en mesure de se déplacer librement et la structure cristalline s'effondre à différents endroits à l'intérieur du cristal.
Une fois que la symétrie de la structure hexagonale est localement cassée, la probabilité d'un autre processus de fusion augmente significativement aux alentours de la zone déjà fondue. Progressivement, c'est toute la glace qui se retrouve affectée, même si, à d'autres endroits, la structure cristalline reste stable un peu plus longtemps.