Le sens des nombres est-il inné ou acquis ?

Psychologue cognitif et neuroscientifique, Stanislas Dehaene s'est spécialisé dans l'étude des bases cérébrales de l'arithmétique et de la numération, mais aussi de la lecture et de la conscience, thèmes qu'il explore par la psychologie cognitive et l'imagerie cérébrale. Directeur de l'Unité mixte Inserm-CEA Neuroimagerie cognitive, il s'est adjoint une équipe composée de chercheurs du CEA, du CNRS et de l'Inserm pour mieux cerner l'architecture cérébrale impliquée dans ces problèmes.

De nombreux travaux réalisés chez des adultes occidentaux mettent en évidence un biais spatial lorsqu'il s'agit d'effectuer une opération arithmétique ou même de penser à un nombre. En effet, la représentation des nombres et celle d'objets dans l'espace sont traitées dans la même zone du cerveaucerveau (au niveau du lobe pariétal), ce qui est vérifiable par IRM fonctionnelleIRM fonctionnelle.

Mais existe-t-il une relation purement intuitive entre les nombres et d'espace ? Stanislas Dehaene vient de répondre par l'affirmative, après avoir poursuivi l'étude commencée par Pierre Pica (CNRS) en 2004 des Indiens d'Amazonie, les Mundurucus, une peuplade dont le lexique des nombres ne dépasse pas 4 ou 5. Bien qu'éprouvant d'insurmontables difficultés à exécuter des opérations arithmétiques élémentaires, les Mundurucus possèdent pourtant une capacité d'approximation comparable à la nôtre.

Un enseignement riche de signification

Les nouvelles recherches démontrent que ces Indiens sont parfaitement capables d'additionner, de soustraire des nombres entre eux, et cela avec une bonne approximation, ce qui était déjà connu. Mais on sait désormais que cette manipulation mathématique s'appuie sur une intuition innée de l'organisation de ces nombres dans l'espace.

Ainsi, si on soumet à un Mundurucu une échelle graduée commençant par le nombre 1 et se terminant par 10 (en symbolisant les nombres par des points dans un cercle) et qu'on leur demande de désigner 2, ils placeront le curseur près du 1. En revanche, ils situent le 5 tout près du 10, tandis que le milieu de l'échelle correspond, selon eux, à 3 ou 4.

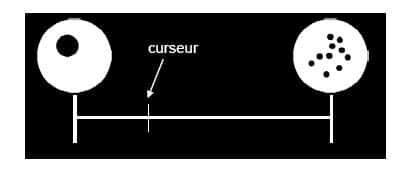
Cette constatation n'est pas anodine, car elle démontre que les Mundurucus se représentent la progression arithmétique comme une suite logarithmique. Plus les nombres sont grands plus ils sont considérés comme proches. Cette intuition, qui peut surprendre un adulte, est en fait commune à tous les humains durant les premières années de la vie.

Chez les Occidentaux, le passage de la représentation logarithmique à la représentation linéaire s'effectue vers 4 à 6 ans. C'est ce que les spécialistes appellent le sens de la mesure, faculté acquise par l'apprentissage. En revanche, un groupe d'adultes occidentaux aura une représentation linéaire des nombres dans l'espace.

En l'absence de cette faculté acquise par l'apprentissage, nous ignorerions qu'il existe un intervalle constant entre 1 et 2, 8 et 9, 1.021 et 1.022. Si cela ne semble pas rédhibitoire chez les Mundurucus ou même d’autres peuplades n'ayant pas usage d'une grande précision dans leurs évaluations, il n'en va pas de même chez nous. D'après les chercheurs, cette découverte doit nous amener à réfléchir sur le rôle essentiel de l'éducation dans l'apprentissage des mathématiques.