Caractéristiques techniques des automates cellulaires

Un automate cellulaire (AC) peut-être décrit par les quatre composantes suivantes.

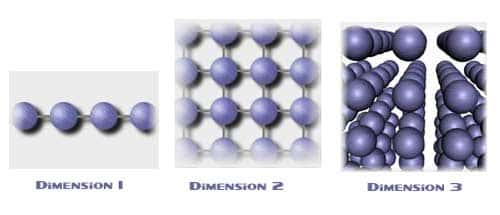
Sa dimension

Le plus générallement 1 (AC élémentaire) ou 2 (AC type Life), il n'y a pas de limite à la dimension d'un automateautomate, si ce n'est la puissance de calcul des machines sensées le reproduire.

Les exemples pratiques d'automates en 3D sont rares. Passé les 3 dimensions, on doit recourir à des projections sur R3 ou R2 pour visualiser correctement l'hyper-matrice.

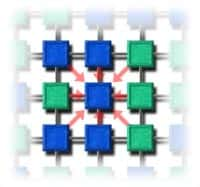
Le voisinage d'une cellule

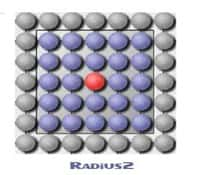
Celui-ci définit l'ensemble des cellules qui auront une influence sur la cellule étudiée. En pratique, le voisinage est souvent limité à la cellule cible et aux cellules adjacentes.

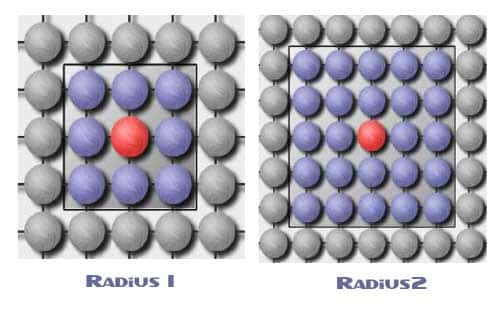
La géométrie des cellules est également étroitement liée à son voisinage. Une cellule peut-être un hyper-cube (cas le plus fréquent), mais également un autre hyper-volume ou désorienté (blind neighbourhood) : un voisinage "aveugle" est un voisinage pour lequel chaque cellule appartenant à ce voisinage joue un rôle identique.

La cellule cible dont on étudie le voisinage a "connaissance" des différents états de ces voisines, mais ne sait pas à quelle cellules correspond quel état.

La plupart des automates cellulairesautomates cellulaires définissent sans le préciser des voisinages "aveugles".

Son espace d'états

Cet espace correspond à l'ensemble des états que peut prendre une cellule. Le plus souvent limité à 2, il n'y a aucune limite théorique. Pour exemple, Von Neumann a étudié mathématiquement un automate à 29 états. Pratiquement, ces états sont représentés par des couleurs, qui permettent de suivre les évolutions de l'automate.

Lors de modélisation de systèmes, les états des cellules correspondent à des états physiquesphysiques locaux. Par exemple, dans le Jeu de la Vie, une cellule est soit "morte" soit "vivante", mais on pourrait très bien imaginer des états transitoires de dégénérescence d'une cellule, en augmentant le nombre d'états de l'automate (cf. life transitoire).

Sa fonction de transition

C'est l'ensemble des règles qui permettent de déterminer le nouvel état d'une cellule en fonction de son état précédent et de l'état précedent de son voisinage. Pour un automate à n états et avec un voisinage de k cellules, il peut y avoir nk configurations de voisinage différentes : 

• pour n=2 et k=3, nk=8 voisinages différents (AC élémentaire de wolfram) ;
• pour n=2 et k=9, nk=512 voisinages différents (jeu de la vie).

De plus, la fonction de transition est créée en associant à chaque voisinage un état de sortie. Il y a donc potentiellement n^nk fonctions de transition pour un automate cellulaire à n états ayant un voisinage de k cellules.

La plupart du temps, ces règles ne sont pas explicitées, mais résumées. Elles sont synthétisées sous la forme de méta-règles (cd règles du jeu de la vie).

La topologie du réseau de cellules

Par exemple, dans le cas d'une matrice 2D, celle-ci peut-être de deux types :

• l'île : les cellules sont entourées virtuellement de cellules mortes.
• le tore : les cellules du bord haut de la matrice sont en contact avec les cellules du bord droit. Idem pour les cellules des bords gauche et droit.